题目内容
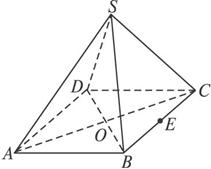
如图,在四棱锥PABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2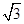 ,E是PB上任意一点.
,E是PB上任意一点.

(1)求证:AC⊥DE;
(2)已知二面角APBD的余弦值为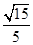 ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.
【答案】
(1)见解析 (2)
【解析】解:(1)证明:∵PD⊥平面ABCD,AC⊂平面ABCD,∴PD⊥AC,
∵四边形ABCD是菱形,∴BD⊥AC,
又BD∩PD=D,∴AC⊥平面PBD,
∵DE⊂平面PBD,∴AC⊥DE.
(2)在△PDB中,EO∥PD,∴EO⊥平面ABCD,分别以OA,OB,OE所在直线为x轴,y轴,z轴建立空间直角坐标系,

设PD=t,则A(1,0,0),B(0, ,0),C(-1,0,0),E
,0),C(-1,0,0),E ,P(0,-
,P(0,- ,t),
,t), =(-1,
=(-1, ,0),
,0), =(-1,-
=(-1,- ,t).
,t).
由(1)知,平面PBD的一个法向量为n1=(1,0,0),设平面PAB的法向量为n2=(x,y,z),则根据
得 令y=1,得平面PAB的一个法向量为n2=
令y=1,得平面PAB的一个法向量为n2= .
.
∵二面角APBD的余弦值为 ,
,
则|cos〈n1,n2〉|= ,
,
即 =
= ,
,
解得t=2 或t=-2
或t=-2 (舍去),
(舍去),
∴P(0,- ,2
,2 ).
).
设EC与平面PAB所成的角为θ,
∵ =(-1,0,-
=(-1,0,- ),n2=(
),n2=( ,1,1),
,1,1),
则sin θ=|cos〈 ,n2〉|=
,n2〉|= =
= ,
,
∴EC与平面PAB所成角的正弦值为 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,且P 为AD的中点,Q为SB的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,且P 为AD的中点,Q为SB的中点.