题目内容
在△ABC中,若cosAcosB-sinAsinB>0,则这个三角形一定是
钝角三角形
钝角三角形
.分析:把已知不等式左边利用二倍角的余弦函数公式变形,得到cos(A+B)的值小于0,由A和B三角形的内角,得到A+B的范围,进而得到A+B为锐角,再根据三角形的内角和定理可得C必须为钝角,故此三角形为钝角三角形.
解答:解:∵cosAcosB-sinAsinB=cos(A+B)>0,且A和B为三角形的内角,
∴0<A+B<90°,又A+B+C=180°,
则C为钝角,即三角形一定是钝角三角形.
故答案为:钝角三角形
∴0<A+B<90°,又A+B+C=180°,
则C为钝角,即三角形一定是钝角三角形.
故答案为:钝角三角形
点评:此题考查了三角形形状的判断,涉及的知识有:两角和与差的余弦函数公式,余弦函数的图象与性质,以及三角形的内角和定理,熟练掌握公式及性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
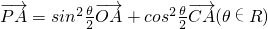 ,则
,则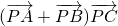 的最小值是________.
的最小值是________.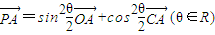 ,则
,则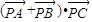 的最小值是 .
的最小值是 .