题目内容
当今世界进入了计算机时代,我们知道计算机装置有一个数据输入口A和一运算结果输出口B,某同学编入下列运算程序,将数据输入且满足以下性质:
①从A输入1时,从B得到
;
②从A输入整数n(n≥2)时,在B得到的结果f(n)是将前一结果f(n-1)先乘以奇数2n-3,再除以奇数2n+1.
(1)求f(2),f(3),f(4);
(2)试由(1)推测f(n)的表达式,并用数学归纳法证明;
(3)求
f(1)+f(2)+…+f(n).
①从A输入1时,从B得到
| 1 |
| 3 |
②从A输入整数n(n≥2)时,在B得到的结果f(n)是将前一结果f(n-1)先乘以奇数2n-3,再除以奇数2n+1.
(1)求f(2),f(3),f(4);
(2)试由(1)推测f(n)的表达式,并用数学归纳法证明;
(3)求
| lim |
| n→∞ |
分析:(1)由已知,得出f(n)=
f(n-1)(n≥2).依次令n=2,3,4可求出f(2),f(3),f(4);
(2)根据(1)的结果,推测并依照数学归纳法进行证明.
(3)f(n)=
裂项为
(
-
).求和后再求极限.
| 2n-3 |
| 2n+1 |
(2)根据(1)的结果,推测并依照数学归纳法进行证明.
(3)f(n)=
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:(1)解:是题意知f(1)=
,f(n)=
f(n-1),
∴当n=2时f(x)=
,
当n=3时f(3)=
,
当n=4时f(4)=
,
猜想f(n)=
.…(3分)
(2)证明:(ⅰ)当n=1时f(1)=
满足f(n)=
.
(ⅱ)假设n=k(k∈N*且k≥1)时,f(k)=
.,
那么n=k+1时,f(k+1)=
f(k)=
×
=
∴n=k+1时也满足f(n)=
.
综上知:f(n)=
.…(8分)
(3)
f(1)+f(2)+…+f(n)=
[
+
+…+
]
=lim
(1-
+
-
+…+
-
)
=
(1-
)=
…(12分)
| 1 |
| 3 |
| 2n-3 |
| 2n+1 |
∴当n=2时f(x)=
| 1 |
| 15 |
当n=3时f(3)=
| 1 |
| 35 |
当n=4时f(4)=
| 1 |
| 63 |
猜想f(n)=
| 1 |
| (2n-1)(2n+1) |
(2)证明:(ⅰ)当n=1时f(1)=
| 1 |
| 3 |
| 1 |
| (2n-1)(2n+1) |
(ⅱ)假设n=k(k∈N*且k≥1)时,f(k)=
| 1 |
| (2n-1)(2n+1) |
那么n=k+1时,f(k+1)=
| 2k-1 |
| 2k+3 |
| 2k-1 |
| 2k+3 |
| 1 |
| (2k-1)(2k+1) |
| 1 |
| [2(k+1)-1][2(k+1)+1] |
∴n=k+1时也满足f(n)=
| 1 |
| (2n-1)(2n+1) |
综上知:f(n)=
| 1 |
| (2n-1)(2n+1) |
(3)
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| (2n-1)(2n+1) |
=lim
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| lim |
| n→∞ |
| 1 |
| 2n+1 |
| 1 |
| 2 |
点评:本题考查阅读、推理、论证、计算能力,借助于数列的递推公式,裂项法求和、极限的知识继续能力考查.

练习册系列答案
相关题目
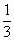 .②从A输入整数n(n≥2)时,从B得到的结果f(n)是将前一结果f(n-1)先乘以奇数2n-3,再除以奇数2n+1.
.②从A输入整数n(n≥2)时,从B得到的结果f(n)是将前一结果f(n-1)先乘以奇数2n-3,再除以奇数2n+1.
 ;
;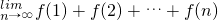 .
. ;
; .
.