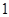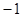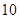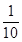题目内容
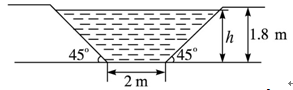
如图,某灌溉渠的横断面是等腰梯形,底宽为2 m,渠深为1.8 m,边坡的倾斜角是45°.
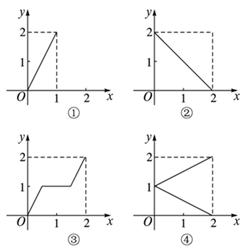
(1)试将横断面中水的面积A(m2)表示成水深h(m)的函数;
(2)确定函数的定义域和值域;
(3)画出函数的图象.

(1)试将横断面中水的面积A(m2)表示成水深h(m)的函数;
(2)确定函数的定义域和值域;
(3)画出函数的图象.
(1) A=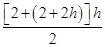 =h2+2h(m2);
=h2+2h(m2);
(2) 定义域为{h|0<h<1.8} 值域为{A|0<A<6.84};
(3)见解析
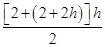 =h2+2h(m2);
=h2+2h(m2);(2) 定义域为{h|0<h<1.8} 值域为{A|0<A<6.84};
(3)见解析
解:(1)由已知,横断面为等腰梯形,下底为2 m,上底为(2+2h) m,高为h m,
∴水的面积A=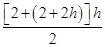 =h2+2h(m2).
=h2+2h(m2).
(2)定义域为{h|0<h<1.8}.值域由二次函数A=h2+2h(0<h<1.8)求得.由函数A=h2+2h=(h+1)2-1的图象可知,在区间(0,1.8)上函数值随自变量的增大而增大,
∴0<A<6.84.
故值域为{A|0<A<6.84}.
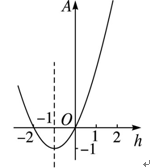
(3)函数图象如下确定.
由于A=(h+1)2-1,对称轴为直线h=-1,顶点坐标为(-1,-1),且图象过(0,0)和(-2,0)两点,又考虑到0<h<1.8,∴A=h2+2h的图象仅是抛物线的一部分,如下图所示.
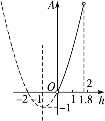
点评:建立函数解析式的关键是找到自变量、对应关系和函数值.对于实际问题,函数的定义域除了使解析式有意义外,还要考虑到它的实际意义.
∴水的面积A=
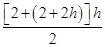 =h2+2h(m2).
=h2+2h(m2).(2)定义域为{h|0<h<1.8}.值域由二次函数A=h2+2h(0<h<1.8)求得.由函数A=h2+2h=(h+1)2-1的图象可知,在区间(0,1.8)上函数值随自变量的增大而增大,
∴0<A<6.84.
故值域为{A|0<A<6.84}.

(3)函数图象如下确定.
由于A=(h+1)2-1,对称轴为直线h=-1,顶点坐标为(-1,-1),且图象过(0,0)和(-2,0)两点,又考虑到0<h<1.8,∴A=h2+2h的图象仅是抛物线的一部分,如下图所示.

点评:建立函数解析式的关键是找到自变量、对应关系和函数值.对于实际问题,函数的定义域除了使解析式有意义外,还要考虑到它的实际意义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
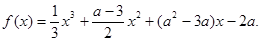
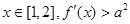 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;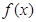 的两个极值点分别为
的两个极值点分别为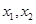 判断下列三个代数式:
判断下列三个代数式: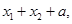 ②
②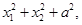 ③
③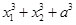 中有几个为定值?并且是定值请求出;
中有几个为定值?并且是定值请求出;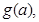 并求出
并求出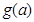 的最小值.
的最小值. 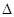 CPD的面积为
CPD的面积为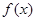 ,则
,则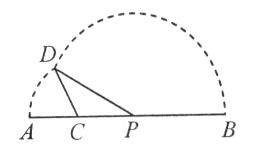
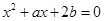 的两根为
的两根为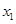 、
、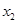 ,且
,且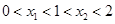 则
则 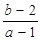 的取值范围是( )
的取值范围是( )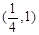
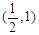
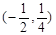

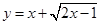 的值域。
的值域。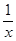
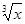
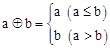 ,则函数
,则函数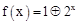 的图象是( )
的图象是( )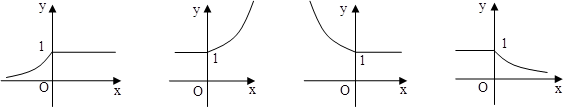
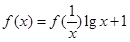 ,则
,则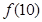 的值为( )
的值为( )