题目内容
【题目】已知椭圆![]() :
:![]() 的左
的左![]() 、
、![]() 右焦点分别为,点
右焦点分别为,点![]() 在椭圆上,且满足
在椭圆上,且满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设倾斜角为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,求
,求![]() 取最大值时直线
取最大值时直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)根据点![]() 在椭圆上,且满足
在椭圆上,且满足![]() ,结合性质
,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() ,即可得椭圆
,即可得椭圆![]() 的方程;(2)设直线
的方程;(2)设直线![]() 的方程为
的方程为![]() .
.
联立 消去
消去![]() ,整理得
,整理得![]() ,由韦达定理,利用弦长公式、点到直线距离公式以及三角形的面积公式求得
,由韦达定理,利用弦长公式、点到直线距离公式以及三角形的面积公式求得![]() ,利用基本不等式可得结果.
,利用基本不等式可得结果.
(1)设![]() ,
,![]() ,根据题意的,
,根据题意的,
![]() ,
,![]() ,
,
所以![]() ,解得
,解得![]() ,
,
因为![]() ,①
,①
又因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,②
,②
联立①②,解得![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)因为直线![]() 的倾斜角为45°,所以设直线
的倾斜角为45°,所以设直线![]() 的方程为
的方程为![]() .
.
联立 消去
消去![]() ,整理得
,整理得
![]()
因为直线![]() 与
与![]() 交于
交于![]() 两点,
两点,
所以![]() ,解得,
,解得,![]() .
.
设![]() ,,则
,,则
![]() ,
,![]() ,
,
从而![]() ,.
,.
又因为点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以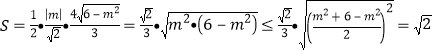 ,
,
当且仅当![]() ,即
,即![]() ,即
,即![]() 时取等号.
时取等号.
所以![]() 的面积
的面积![]() 的最大值为
的最大值为![]() ,
,
此时直线![]() 的方程为
的方程为![]() 或
或![]() .
.

 习题精选系列答案
习题精选系列答案【题目】给出下面几种说法:
①相等向量的坐标相同;
②若向量![]() 满足
满足![]() ,则
,则![]()
③若![]() ,
,![]() ,
,![]() ,
,![]() 是不共线的四点,则“
是不共线的四点,则“![]() ”是“四边形
”是“四边形![]() 为平行四边形”的充要条件;
为平行四边形”的充要条件;
④![]() 的充要条件是
的充要条件是![]() 且
且![]() .
.
其中正确说法的个数是( )
A.1B.2C.3D.4
【题目】某单位为促进职工业务技能提升,对该单位120名职工进行一次业务技能测试,测试项目共5项.现从中随机抽取了10名职工的测试结果,将它们编号后得到它们的统计结果如下表(表1)所示(“√”表示测试合格,“×”表示测试不合格).
表1:
编号\测试项目 | 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
规定:每项测试合格得5分,不合格得0分.
(1)以抽取的这10名职工合格项的项数的频率代替每名职工合格项的项数的概率.
①设抽取的这10名职工中,每名职工测试合格的项数为![]() ,根据上面的测试结果统计表,列出
,根据上面的测试结果统计表,列出![]() 的分布列,并估计这120名职工的平均得分;
的分布列,并估计这120名职工的平均得分;
②假设各名职工的各项测试结果相互独立,某科室有5名职工,求这5名职工中至少有4人得分不少于20分的概率;
(2)已知在测试中,测试难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 项测试难度,
项测试难度,![]() 为第
为第![]() 项合格的人数,
项合格的人数,![]() 为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
表2:
测试项目 | 1 | 2 | 3 | 4 | 5 |
实测合格人数 | 8 | 8 | 7 | 7 | 2 |
定义统计量![]() ,其中
,其中![]() 为第
为第![]() 项的实测难度,
项的实测难度,![]() 为第
为第![]() 项的预测难度(
项的预测难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
表3:
测试项目 | 1 | 2 | 3 | 4 | 5 |
预测前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
判断本次测试的难度预估是否合理.