题目内容
(本题12分)某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3m2,可做文字标牌1个,绘画标牌2个,乙种规格每张2m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?

【答案】
解:设需要甲种原料x张,乙种原料y张,
则可做文字标牌(x+2y)个,绘画标牌(2x+y)个.
由题意可得:
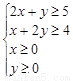 …………5分
…………5分
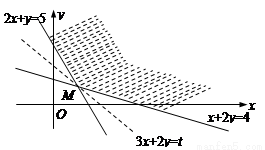
所用原料的总面积为z=3x+2y,作出可行域如图,…………8分
在一组平行直线3x+2y=t中,经过可行域内的点且到原点距离最近的直线
过直线2x+y=5和直线x+2y=4的交点(2,1),∴最优解为:x=2,y=1………10分
∴使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小.………12分
【解析】略

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
(本小题满分12分)
某人射击一次命中7~10环的概率如下表
| 命中环数 | 7 | 8 | 9 | 10 |
| 命中概率 | 0.16 | 0.19 | 0.28 | 0.24 |
计算这名射手在一次 射击中:
(1)射中9环或10环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率
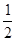 ,构造数列
,构造数列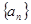 ,使
,使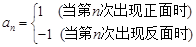 ,记
,记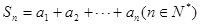 .
.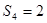 的概率;
的概率;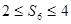 的概率.
的概率.