题目内容
在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρ=4cosθ,直线l的参数方程是 (t为参数).
(t为参数).(1)求极点在直线l上的射影点P的极坐标;
(2)若M、N分别为曲线C、直线l上的动点,求|MN|的最小值.
【答案】分析:(1)由直线的参数方程设设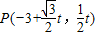 ,得向量
,得向量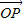 的坐标,再利用它与l的一个方向向量垂直得到一个关于参数t的方程,解得t值,最后将P的坐标化成极坐标即可;
的坐标,再利用它与l的一个方向向量垂直得到一个关于参数t的方程,解得t值,最后将P的坐标化成极坐标即可;
(2)欲求|MN|的最小值,即求出圆上一点何时到直线的距离最小,先转化为圆心到直线的距离最小值求解,结合直角坐标系下的点到直线的距离公式求解即得.
解答:解:(1)由直线的参数方程消去参数t得l: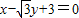 ,
,
则l的一个方向向量为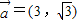 ,
,
设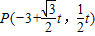 ,
,
则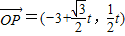 ,
,
又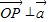 ,
,
则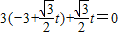 ,得:
,得: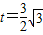 ,
,
将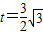 代入直线l的参数方程得
代入直线l的参数方程得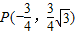 ,
,
化为极坐标为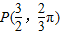 .
.
(2)ρ=4cosθ⇒ρ2=4ρcosθ,
由ρ2=x2+y2及x=ρcosθ得(x-2)2+y2=4,
设E(2,0),则E到直线l的距离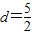 ,
,
则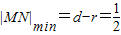 .
.
点评:本题考查点的极坐标、直线的参数方程和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.
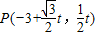 ,得向量
,得向量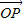 的坐标,再利用它与l的一个方向向量垂直得到一个关于参数t的方程,解得t值,最后将P的坐标化成极坐标即可;
的坐标,再利用它与l的一个方向向量垂直得到一个关于参数t的方程,解得t值,最后将P的坐标化成极坐标即可;(2)欲求|MN|的最小值,即求出圆上一点何时到直线的距离最小,先转化为圆心到直线的距离最小值求解,结合直角坐标系下的点到直线的距离公式求解即得.
解答:解:(1)由直线的参数方程消去参数t得l:
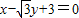 ,
,则l的一个方向向量为
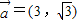 ,
,设
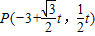 ,
,则
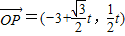 ,
,又
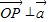 ,
,则
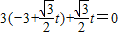 ,得:
,得: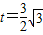 ,
,将
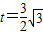 代入直线l的参数方程得
代入直线l的参数方程得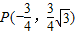 ,
,化为极坐标为
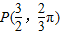 .
.(2)ρ=4cosθ⇒ρ2=4ρcosθ,
由ρ2=x2+y2及x=ρcosθ得(x-2)2+y2=4,
设E(2,0),则E到直线l的距离
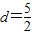 ,
,则
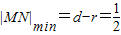 .
.点评:本题考查点的极坐标、直线的参数方程和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.

练习册系列答案
相关题目