题目内容
(本小题满分13分)已知函数
(I)求函数f(x)的最小正周期和单调增区间;
(Ⅱ)函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
(1)f(x)的最小正周期T=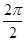 =π.
=π.
f(x)的单调增区间为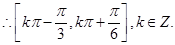
(2)见解析
解析试题分析:(1)利用三角函数的恒等变换化简f(x)的解析式为 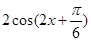 ,由此求得函数的最小正周期,及单调增区间
,由此求得函数的最小正周期,及单调增区间
(2)平移有两种思路:一是先平移再伸缩,二是先伸缩再平移.
(1)f(x)=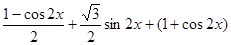
=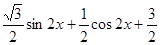
=sin(2x+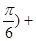
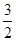 .
.
∴f(x)的最小正周期T=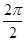 =π.
=π.
由题意得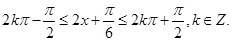
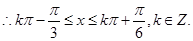
∴f(x)的单调增区间为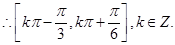
(2)方法一:
先把y="sin" 2x图象上所有的点向左平移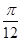 个单位长度,得到y=sin(2x+
个单位长度,得到y=sin(2x+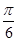 )的图象,再把所得图象上所有的点向上平移
)的图象,再把所得图象上所有的点向上平移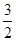 个单位年度,就得到y=sin(2x+
个单位年度,就得到y=sin(2x+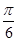 )+
)+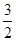 的图象.
的图象.
方法二:
把y="sin" 2x图象上所有的点按向量a=(-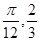 )平移,就得到y=sin(2x+
)平移,就得到y=sin(2x+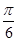 )+
)+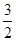 的图象.
的图象.
考点:三角函数中的恒等变换应用;三角函数的周期性及其求法;复合三角函数的单调性.
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性以及求法,求三角函数的单调区间,图像变换等.属于中档题.

练习册系列答案
相关题目
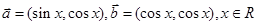 ,函数
,函数 .
. 的最大值与最小正周期;
的最大值与最小正周期;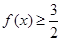 成立的
成立的 的取值范围.
的取值范围.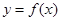
 .
.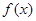 的最小正周期和最大值;
的最小正周期和最大值;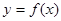 在区间
在区间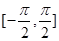 上的图象.
上的图象.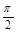 ,且方程
,且方程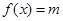 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 始终为
始终为 (其中点P,Q分别在边BC,CD上),设
(其中点P,Q分别在边BC,CD上),设 .
.

 的周长l是否为定值;
的周长l是否为定值; ,
, ,设函数
,设函数
 的图象关于直线
的图象关于直线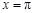 对称,其中
对称,其中 ,
, 为常数,且
为常数,且 .
.  的最小正周期;
的最小正周期; 的图象经过点
的图象经过点 ,求函数
,求函数 上的取值范围.
上的取值范围. ,设函数
,设函数

 的最小正周期及单调递增区间;(2)当
的最小正周期及单调递增区间;(2)当 时,求
时,求 上是增函数,
上是增函数, ,
,
 时,求
时,求 的值;
的值; 的最值以及
的最值以及 (其中
(其中 )的图象与
)的图象与 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为 ,
, 的解析式 (2).当
的解析式 (2).当 时,求
时,求 ,求
,求 时函数
时函数 的最值。
的最值。