题目内容

已知直线y=x-1与双曲线交于两点M，N 线段MN的中点横坐标为- $数学公式$ 双曲线焦点c为 $数学公式$ ，则双曲线方程为________．

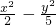$\text{[math]}$ =1
分析：先设出曲线的方程，和M，N的坐标，分别代入直线方程相减求得y₁-y₂=x₁-x₂，利用MN中点的横坐标求得x₁+x₂，利用直线方程求得y₁+y₂，把M，N代入双曲线方程相减求得a和b的关系，进而利用c求得a和b，则双曲线的方程可得．
解答：设双曲线 $\text{[math]}$ =1，M，N （x₁，y₁）（x₂，y₂）
则y₁=x₁-1，y₂=x₂-1，两式相减求得y₁-y₂=x₁-x₂，
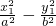$\text{[math]}$ =1， $\text{[math]}$ =1
两式相减得：
$\text{[math]}$ =0
又因为x₁+x₂=- $\text{[math]}$
y₁+y₂=x₁+x₂-2=- $\text{[math]}$
∵y₁-y₂=x₁-x₂
所以 $\text{[math]}$ = $\text{[math]}$
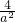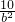
∵c= $\text{[math]}$ = $\text{[math]}$
求得a= $\text{[math]}$ ，b= $\text{[math]}$
∴双曲线方程为 $\text{[math]}$ =1
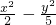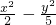故答案为： $\text{[math]}$ =1
点评：本题主要考查了直线与圆锥曲线的综合问题．涉及弦的中点及中点弦问题，利用差分法较为简便．

练习册系列答案

三维导学案系列答案

单元双测试卷系列答案

活页练习西安出版社系列答案

作业课课清系列答案

轻松15分达标作业系列答案

节节高解析测评系列答案

海淀金卷系列答案

全能金卷全能卷王系列答案

名师优选全程练考卷系列答案

本真试卷系列答案

相关题目

已知直线y=x+1与椭圆（m＞n＞0）相交于A，B两点，若弦AB中点的横坐标为-

，则双曲线

=1的两条渐近线夹角的正切值是

已知直线y=x-1与双曲线交于两点M，N 线段MN的中点横坐标为-

双曲线焦点c为

，则双曲线方程为

已知直线y=x-1与曲线y=ln（x+a）相切，则a的值为（　　）

已知直线y=-x+1与椭圆

=1(a＞0，b＞0)相交于A、B两点．
（1）若椭圆的离心率为

，焦距为2，求线段AB的长；
（2）若向量

互相垂直（其中O为坐标原点），当椭圆的离心率e∈[

]时，求椭圆的长轴长的最大值．

已知直线y=-x+1与椭圆

=1 (a＞b＞0)相交于A，B两点，且OA⊥OB（O为坐标原点），若椭圆的离心率e∈[

]，则a的最大值为