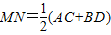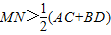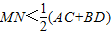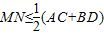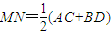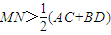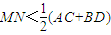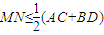Question

设线段AB，CD是夹在两平行平面α，β间的两异面线段，点A，C∈α，B，D∈β，若M，N分别为AB，CD的中点，则有（　　）

• A、MN=

  1

  2

  (AC+BD)
• B、MN＞

  1

  2

  (AC+BD)
• C、MN＜

  1

  2

  (AC+BD)
• D、MN≤

  1

  2

  (AC+BD)

Answer 1

分析：利用中位线定理将AC与BD平移到AD的中点E处，再根据三角形中任意两边之和大于第三边即可得到结论．

解答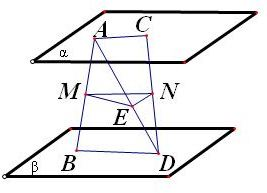：解：如图
连接AD，取AD的中点E，连接ME，NE
ME=

1

2

BD，EN=

1

2

AC，而MN＜ME+EN
即MN＜

1

2

(AC+BD)，
故选C

点评：本题主要考查了异面直线及其所成的角，以及平面的基本性质及推论，属于基础题．