Question

若函数f（x）为定义在R上的奇函数，且x∈（0，+∞）时，f（x）=2^x
（1）求f（x）的表达式；
（2）在所给的坐标系中直接画出函数f（x）图象．（不必列表）

Answer 1

分析：（1）先利用奇函数的性质计算f（0），再利用奇函数的定义，求当x∈（-∞，0）时，函数的解析式，最后利用分段函数写出函数解析式
（2）利用奇函数的对称性，先画出x＞0时的图象，在关于原点对称即可得函数图象，注意原点也在函数图象上

解答：解：（1）∵f（x）为定义在R上的奇函数，
∴f（0）=0
当x∈（-∞，0）时，-x∈（0，+∞），则f（-x）=2^-x
又f（x）为定义在R上的奇函数，
∴f（-x）=-f（x），则f（x）=-f（-x）=-2^-x
∴f（x）=

2x    x∈ (0，+∞) 0      x=0 -2-x    x∈(-∞，0)

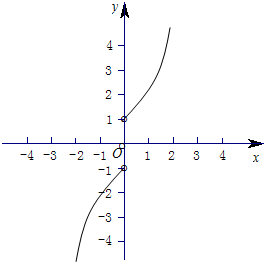
（2）f（x）的图象如图：

点评：本题考查了奇函数的定义及其应用，利用奇函数的对称性求函数的解析式和画图象的方法，分段函数的意义