题目内容
已知α,β均为锐角,且sinα=
,sin(α-β)=-
.
(1)求tan(α-β)的值;
(2)求cosβ的值.
| 3 |
| 5 |
| ||
| 10 |
(1)求tan(α-β)的值;
(2)求cosβ的值.
(1)∵α,β∈(0,
),∴-
<α-β<
.…(2分)
又sin(α-β)=-
,∴-
<α-β<0…(4分)
∴cos(α-β)=
,∴tan(α-β)=-
…(7分)
(2)∵α为锐角,sinα=
,∴cosα=
.…(8分)
∴cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)…(12分)
=
×
+
×(-
)=
.…(14分)
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
又sin(α-β)=-
| ||
| 10 |
| π |
| 2 |
∴cos(α-β)=
3
| ||
| 10 |
| 1 |
| 3 |
(2)∵α为锐角,sinα=
| 3 |
| 5 |
| 4 |
| 5 |
∴cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)…(12分)
=
| 4 |
| 5 |
3
| ||
| 10 |
| 3 |
| 5 |
| ||
| 10 |
9
| ||
| 50 |

练习册系列答案
相关题目
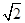 cosx(m>0)的最大值为2.
cosx(m>0)的最大值为2. 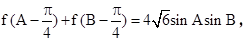 角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积. 中,若
中,若 ,则
,则 与
与 的大小关系为( )
的大小关系为( )



 ,求
,求 的值;
的值; 

 求
求 的值.
的值. 中
中 ,则
,则 等于
等于