Question

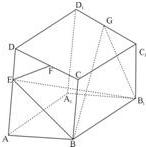如图，在直四棱柱ABCD-A₁B₁C₁D₁中，底面ABCD是梯形BC∥AD，∠DAB=90°，AB=BB₁=4，BC=3，AD=5，AE=3，F、G分别为CD、C₁D₁的中点．
（1）求证：EF⊥平面BB₁G；
（2）求二面角E-BB₁-G的大小．

Answer 1

分析：（1），要证明线面垂直，根据判定定理，需要证明直线垂直于EF平面BB₁G内的两条相交直线，由直四棱柱的性质容易证明EF⊥BB₁，所以只需证明EF⊥BF，二者在同一个平面内，故只需连接BF并延长与AD的延长线交于点H，通过三角形全等证明EF⊥BF即可．
（2），求二面角的思路有两条，一：作、证、指、求，作出二面角的平面角，再去利用解三角形的方法，或者建立空间直角坐标系，利用向量的夹角来解决．

解答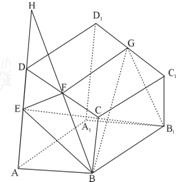：解：（1）连接FG∵F、G分别为CD、C₁D₁的中点，
∴FG∥CC₁且相等， ;；；从而FG∥BB₁ 且相等
 ;；；∴B、B₁、F、G四点共面．
连接BF并延长与AD的延长线交于点H．
∵F为CD的中点，且BC∥AD．
∴△HFD≌△BFC∴DH=BC=3
∴EH=DE+DH=5．又∵BE=5，且F为BH的中点．
∴EF⊥BF，又∵BB₁⊥平面ABCD，且EF?平面ABCD内．
∴BB₁⊥EF∴EF⊥平面BB₁GF．从而EF⊥平面BB₁G．

（2）二面角E-BB₁-G的大小等于二面角F-BB₁-E的大小
∵EF⊥平面FBB₁且EB⊥BB₁FB⊥BB₁
即∠EBF为二面角F-BB₁-E的平面角
在△EFB中，EB=5，EF=

1

2

DC=

5

．∴sin∠EBF=

5

5

∴∠EBF=arcsin

5

5

∴二面角E-BB₁-G的大小为arcsin

5

5

解法2：以A为坐标原点，AB为x轴，AA₁为y轴，AD为Z轴建立空间直角坐标系，
则E（0，0，3）、F（2，0，4）、G（2，4，4）、B（4，0，0）、B₁（4，4，0）
（1）

EF

=(2，0，1)、

BB1

=(0，4，0)、

B1G

=(-2，0，4)
∵

EF

•

BB1

=0，

EF

•

B1G

=-4+4=0
∴EF⊥BB₁，EF⊥B₁G∴EF⊥平面BB₁G
（2）∵EF⊥平面BB₁G∴

EF

=(2，0，1)为平面BB₁G的一个法向量
设平面EBB₁的一个法向量为

n

=(x，y，z)

BE

=(-4，0，3)

BB1

=(0，4，0)
则

n • BE =-4x+3z=0 n • BB1 =4y=0

解得y=0，取z=4
∴

n

=(3，0，4)cos＜

EF

•

n

＞=

EF • n

| EF |•| n |

=

10

5 ×5

=

2 5

5

∴二面角E-BB₁-G的大小为arccos

2 5

5

点评：本题考查线面垂直的证明和二面角的求法，是高考的热点和重点，在证明中要注意转化思想的应用，将证明线面垂直转化为证线线垂直，求二面角两种方法要注意几何法中的作角，向量法中要注意选取两个平面的法向量，也可以在两个平面内选取，但是要注意他们的夹角与二面角的关系．