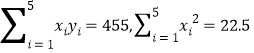题目内容
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 有相同的焦点
有相同的焦点![]() 为原点,点
为原点,点![]() 是准线上一动点,点
是准线上一动点,点![]() 在抛物线上,且
在抛物线上,且![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
【答案】![]()
【解析】∵椭圆![]() ,a=
,a=![]() ,b=1,则c2=5﹣1=4,即c=2,
,b=1,则c2=5﹣1=4,即c=2,
则椭圆的焦点为(0,±2),
不妨取焦点(0,2),
∵抛物线x2=ay,
∴抛物线的焦点坐标为(0, ![]() ),
),
∵椭圆![]() 与抛物线
与抛物线![]() 有相同的焦点
有相同的焦点![]() ,
,
∴![]() =2,即a=8,则抛物线方程为x2=8y,准线方程为y=﹣2,
=2,即a=8,则抛物线方程为x2=8y,准线方程为y=﹣2,
∵|AF|=4,由抛物线的定义得,
∴A到准线的距离为4,y+2=4,
即A点的纵坐标y=2,
又点A在抛物线上,
∴x=±4,不妨取点A的坐标A(4,2);
A关于准线的对称点的坐标为B(4,﹣6)
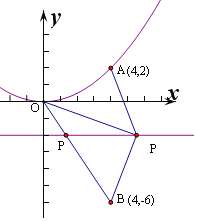
则|PA|+|PO|=|PB|+|PO|≥|OB|,
即O,P,B三点共线时,有最小值,
最小值为|AB|=![]() =
=![]() ,
,
故答案为: ![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用![]() (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人![]() (万元)的数据如下表:
(万元)的数据如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促销费用 |
|
|
|
|
|
销售收入 |
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出/span>![]() 关于
关于![]() 的线性回归方
的线性回归方![]() ;
;
(2)2018年度该店铺预测销售收人至少达到![]() 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?
参考公式: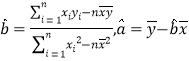
参考数据: