题目内容
6.设数列{an}的前项和为Sn,a1=1,an=$\frac{S_n}{n}+2(n-1),(n∈{N^*})$.(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)是否存在正整数n使得$\frac{S_1}{1}+\frac{S_2}{2}$+…+$\frac{S_n}{n}-{(n-1)^2}$=2015成立?若存在,求出n的值;若不存在,请说明理由.
分析 (I)利用已知条件求出Sn=nan-2(n-1)n,利用an=Sn-Sn-1,推出an-an-1=4,判断{an}为等差数列,求解通项公式.
(II)利用第一问以及已知条件推出$\frac{{S}_{n}}{n}=2n-1$,求出数列的和,然后求解方程判断即可.
解答 解:(I)数列{an}的前项和为Sn,a1=1,an=$\frac{S_n}{n}+2(n-1),(n∈{N^*})$.
所以Sn=nan-2(n-1)n,
n≥2时,an=Sn-Sn-1=nan-2(n-1)n-(n-1)an-1+2(n-2)(n-1)
可得an-an-1=4
所以{an}为a1=1,d=4的等差数列
所以an=1+(n-1)4=4n-3…(6分)
(II)∵an=4n-3,
∴${S_n}=n{a_n}-2n(n-1)=(2n-1)n⇒\frac{S_n}{n}=2n-1$
$⇒\frac{S_1}{1}+\frac{S_2}{2}+…+\frac{S_n}{n}=\frac{1+(2n-1)}{2}n={n^2}$
⇒n2-(n-1)2=2015
⇒n=1008存在 …(12分)
点评 本题考查数列的递推关系式以及数列求和,考查计算能力.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
16.已知数列{an}满足a1=1,|an-an-1|=$\frac{1}{{3}^{n}}$(n∈N,n≥2),且{a2n-1}是递减数列,{a2n}是递增数列,则12a10=( )
| A. | 6-$\frac{1}{{3}^{10}}$ | B. | 6-$\frac{1}{{3}^{9}}$ | C. | 11-$\frac{1}{{3}^{10}}$ | D. | 11-$\frac{1}{{3}^{9}}$ |
14.若$z=\frac{i}{1+2i}$,i为虚数单位,则|z|=( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
11.若函数$f(x)=2sin(ωx+\frac{π}{3})$,且f(α)=-2,f(β)=0,|α-β|的最小值是$\frac{π}{2}$,则f(x)的单调递增区间是( )
| A. | $[kπ-\frac{5π}{12},kπ+\frac{π}{12}]\;\;(k∈Z)$ | B. | $[kπ-\frac{π}{3},kπ+\frac{π}{6}]\;\;(k∈Z)$ | ||
| C. | $[2kπ-\frac{2π}{3},2kπ+\frac{π}{3}]\;\;(k∈Z)$ | D. | $[2kπ-\frac{5π}{6},2kπ+\frac{π}{6}]\;(\;k∈Z)$ |
15.程序框图如图所示,若其输出结果是30,则判断框中填写的是( )
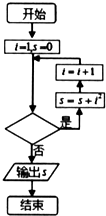

| A. | i<7? | B. | i<5? | C. | i>7? | D. | i>5? |
 如图是一个几何体的三视图,若它的体积是$3\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.
如图是一个几何体的三视图,若它的体积是$3\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.


