题目内容
若复数x+yi满足:x+yi=
(x,y∈R,i是虚数单位),则
=( )
| 2-i |
| 2+i |
| y |
| x |
分析:x+yi=
,
=
-
i.根据复数相等的意义,得x=
,y=-
,由此能求出
的值.
| 2-i |
| 2+i |
| 2-i |
| 2+i |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| y |
| x |
解答:解:∵x+yi=
=
=
=
=
-
i.
根据复数相等的意义,得x=
,y=-
,
∴
=
=-
.
故选A.
| 2-i |
| 2+i |
=
| (2-i)2 |
| (2+i)(2-i) |
=
| 4-4i+i2 |
| 4-i2 |
=
| 3-4i |
| 5 |
=
| 3 |
| 5 |
| 4 |
| 5 |
根据复数相等的意义,得x=
| 3 |
| 5 |
| 4 |
| 5 |
∴
| y |
| x |
| ||
-
|
| 4 |
| 3 |
故选A.
点评:本题考查复数的代数形式的乘除运算,是基础题.解题时要认真审题,注意复数相等的充要条件的灵活运用.

练习册系列答案
相关题目
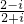 (x,y∈R,i是虚数单位),则
(x,y∈R,i是虚数单位),则 =
=

 (x,y∈R,i是虚数单位),则
(x,y∈R,i是虚数单位),则 =( )
=( )


