题目内容
从4名教师与5名学生中任选3人，其中至少要有教师与学生各1人，则不同的选法共有________种．
70
满足题设的情形分为以下2类：
第一类，从4名教师选1人，又从5名学生中任选2人，有C41C52种不同选法；
第二类，从4名教师选2人，又从5名学生中任选1人，有C42C51种不同选法．
因此共有C41C52＋C42C51＝70(种)不同的选法．
第一类，从4名教师选1人，又从5名学生中任选2人，有C41C52种不同选法；
第二类，从4名教师选2人，又从5名学生中任选1人，有C42C51种不同选法．
因此共有C41C52＋C42C51＝70(种)不同的选法．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
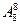
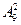
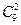
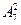
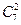
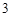个项目的比赛安排在
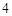个不同的体育馆举办，每个项目的比赛只能安排在一个体育馆进行，则在同一个体育馆比赛的项目不超过
个的安排方案共有（ ）
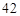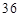种
种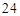
种
种