题目内容
【题目】班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.
(1)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可,不必计算出结果)
(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
数学成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
物理成绩 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
①若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②根据上表数据,求物理成绩![]() 关于数学成绩
关于数学成绩![]() 的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
附:线性回归方程![]() ,
,
其中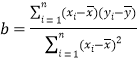 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |
【答案】(1)不同的样本的个数为![]() .
.
(2)①分布列见解析,![]()
![]() .
.
②线性回归方程为![]() .可预测该同学的物理成绩为96分.
.可预测该同学的物理成绩为96分.
【解析】
(1)按比例抽取即可,再用乘法原理计算不同的样本数.
(2)![]() 名学生中物理和数学都优秀的有3名学生,任取3名学生,都优秀的学生人数
名学生中物理和数学都优秀的有3名学生,任取3名学生,都优秀的学生人数![]() 服从超几何分布,故可得其概率分布列及其数学期望.而线性回归方程的计算可用给出的公式计算,并利用得到的回归方程预测该同学的物理成绩.
服从超几何分布,故可得其概率分布列及其数学期望.而线性回归方程的计算可用给出的公式计算,并利用得到的回归方程预测该同学的物理成绩.
(1)依据分层抽样的方法,24名女同学中应抽取的人数为![]() 名,
名,
18名男同学中应抽取的人数为![]() 名,
名,
故不同的样本的个数为![]() .
.
(2)①∵7名同学中数学和物理成绩均为优秀的人数为3名,
∴![]() 的取值为0,1,2,3.
的取值为0,1,2,3.
∴![]() ,
,![]() ,
,
![]() ,
,![]() .
.
∴![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴![]() .
.
②∵![]() ,
,![]() .
.
∴线性回归方程为![]() .
.
当![]() 时,
时,![]() .
.
可预测该同学的物理成绩为96分.

 名校课堂系列答案
名校课堂系列答案【题目】据报道,某公司的33名职工的月工资(以元为单位)如下:
职务 | 董事长 | 副董事长 | 董事 | 总经理 | 经理 | 管理员 | 职员 |
人数 | 1 | 1 | 2 | 1 | 5 | 3 | 20 |
工资 | 5500 | 5500 | 3500 | 3000 | 2500 | 2000 | 1500 |
(1)求该公司职工月工资的平均数(精确到元);
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数又是什么?(精确到元)
(3)你认为工资的平均数能反映这个公司员工的工资水平吗?结合此问题谈一谈你的看法.
【题目】某校团委对“学生性别与中学生追星是否有关”作了一次调查,利用![]() 列联表,由计算得
列联表,由计算得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
得到正确结论是( )
A. 有99%以上的把握认为“学生性别与中学生追星无关”
B. 有99%以上的把握认为“学生性别与中学生追星有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星无关”
D. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星有关”
