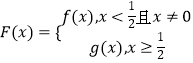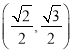题目内容
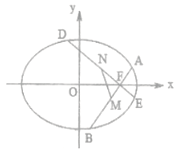
【题目】如图,函数y=f(x)的图像为折线ABC,设g (x)=f[f(x)],则函数y=g(x)的图像为( )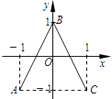
A.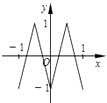
B.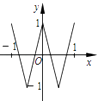
C.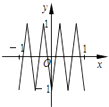
D.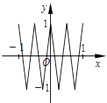
【答案】A
【解析】解:如图:函数y=f(x)的图像为折线ABC,函数f(x)为偶函数,
我们可以研究x≥0的情况即可,
若x≥0,可得B(0,1),C(1,﹣1),这直线BC的方程为:lBC:y=﹣2x+1,x∈[0,1],其中﹣1≤f(x)≤1;
若x<0,可得lAB:y=2x+1,∴f(x)= ![]() ,
,
我们讨论x≥0的情况:如果0≤x≤ ![]() ,解得0≤f(x)≤1,此时g(x)=f[f(x)]=﹣2(﹣2x+1)+1=4x﹣1;
,解得0≤f(x)≤1,此时g(x)=f[f(x)]=﹣2(﹣2x+1)+1=4x﹣1;
若 ![]() <x≤1,解得﹣1≤f(x)<0,此时g(x)=f[f(x)]=2(﹣2x+1)+1=﹣4x+3;
<x≤1,解得﹣1≤f(x)<0,此时g(x)=f[f(x)]=2(﹣2x+1)+1=﹣4x+3;
∴x∈[0,1]时,g(x)= 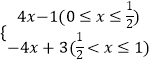 ;
;
故选A;
【考点精析】掌握函数的偶函数是解答本题的根本,需要知道一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】设全集U={(x,y)|x,y∈R},集合M={(x,y)| ![]() =1},N={(x,y)|y=x+1},则N∩(UM)等于( )
=1},N={(x,y)|y=x+1},则N∩(UM)等于( )
A.
B.{(2,3)}
C.(2,3)
D.{(x,y)|y=x+1}
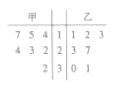
【题目】某厂商为了解用户对其产品是否满意,在使用产品的用户中随机调查了80人,结果如下表:

(1)根据上述,现用分层抽样的方法抽取对产品满意的用户5人,在这5人中任选2人,求被选中的恰好是男、女用户各1人的概率;
(2)有多大把握认为用户对该产品是否满意与用户性别有关?请说明理由.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注:![]()