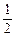题目内容
(本小题共12分)设x=3是函数f (x) = (x2+ax+b)·e3-x (x∈R)的一个极值点。
⑴求a与b的关系式,(用a表示b),并求f(x)的单调区间。
⑵设a>0,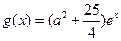 ,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围。
,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围。
⑴求a与b的关系式,(用a表示b),并求f(x)的单调区间。
⑵设a>0,
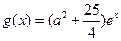 ,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围。
,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围。(1)略
(2)a的取值范围是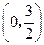 。
。
(2)a的取值范围是
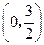 。
。 解:⑴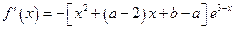 (2分)
(2分)
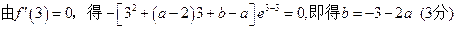
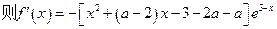
=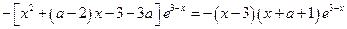
令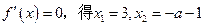
由于x=3是极值点,所以3+a+1≠0,那么a≠-4。
当a<-4时,x2>3=x1,则在区间(-∞,3)上,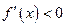 ,f(x)为减函数;
,f(x)为减函数;
在区间(3,-a-1 )上
)上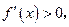 f (x)为增函数。
f (x)为增函数。
在区间(-a-1,+∞) 上
上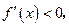 f (x)为减函数。 (4分)
f (x)为减函数。 (4分)
当a>-4时,x2<3=x1,则在区间(-∞,-a-1)上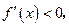 f(x)为减函数;
f(x)为减函数;
在区间(-a-1,3)上, 为增
为增 函数;
函数;
在区间(3 ,+∞)上,
,+∞)上,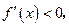 f(x)
f(x) 为减函数。 (6分)
为减函数。 (6分)
⑵由①知,当a>0时,f(x)在区间(0,3)上的单调递增,在区间(3,4)上单调递减,
那么f(x)在区间[0,4]上的值域是[min (f (0),f (4)),f (3)],
而f (0)=-(2a+3)e3<0,f (4)=(2a+13)e-1>0,f(3)=a+6,
那么f(x)在区间[0,4]上的值域是[-(2a+3)e3,a+6], (8分)
又g (x)=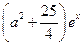 在区
在区 间[0,4]上是增函数,
间[0,4]上是增函数,
且它在区间[0,4]上的值域是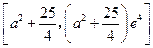 (10分)
(10分)
由于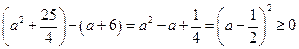
所以只需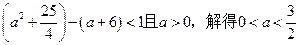

故a的取值范围是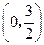 。
。  (12分)
(12分)
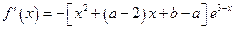 (2分)
(2分)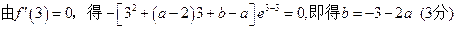
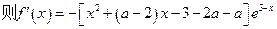
=
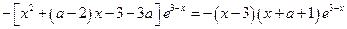
令
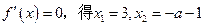
由于x=3是极值点,所以3+a+1≠0,那么a≠-4。
当a<-4时,x2>3=x1,则在区间(-∞,3)上,
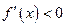 ,f(x)为减函数;
,f(x)为减函数;在区间(3,-a-1
 )上
)上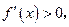 f (x)为增函数。
f (x)为增函数。在区间(-a-1,+∞)
 上
上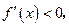 f (x)为减函数。 (4分)
f (x)为减函数。 (4分)当a>-4时,x2<3=x1,则在区间(-∞,-a-1)上
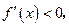 f(x)为减函数;
f(x)为减函数;在区间(-a-1,3)上,
 为增
为增 函数;
函数;在区间(3
 ,+∞)上,
,+∞)上,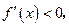 f(x)
f(x) 为减函数。 (6分)
为减函数。 (6分)⑵由①知,当a>0时,f(x)在区间(0,3)上的单调递增,在区间(3,4)上单调递减,
那么f(x)在区间[0,4]上的值域是[min (f (0),f (4)),f (3)],
而f (0)=-(2a+3)e3<0,f (4)=(2a+13)e-1>0,f(3)=a+6,
那么f(x)在区间[0,4]上的值域是[-(2a+3)e3,a+6], (8分)
又g (x)=
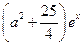 在区
在区 间[0,4]上是增函数,
间[0,4]上是增函数,且它在区间[0,4]上的值域是
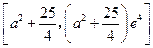 (10分)
(10分)由于
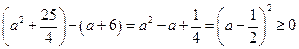
所以只需
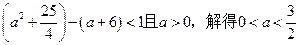

故a的取值范围是
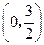 。
。  (12分)
(12分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
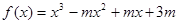 在
在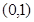 内有极大值,无极小值,则
内有极大值,无极小值,则



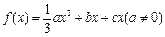 ,已知
,已知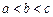 ,且
,且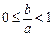 ,曲线
,曲线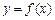 在x=1处取极值.
在x=1处取极值.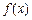 的递增区间为
的递增区间为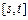 ,求
,求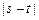 的取值范围; (Ⅱ)如果当
的取值范围; (Ⅱ)如果当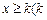 是与
是与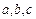 无关的常数
无关的常数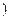 时,恒有
时,恒有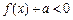 ,求实数
,求实数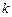 的最小值
的最小值 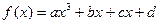 的图象与y轴的交点为点P,且曲线在点P处的切线方程为
的图象与y轴的交点为点P,且曲线在点P处的切线方程为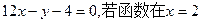 处取得极值0,试求函数的单调区间。
处取得极值0,试求函数的单调区间。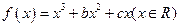 ,已
,已 知
知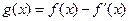
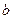 、
、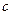 的值;
的值;  的单调区间与极值.
的单调区间与极值.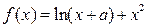
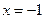 时,
时,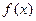 取得极值,求
取得极值,求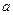 的值,并讨论
的值,并讨论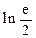 .
. ,若
,若 ,则
,则 的最小值为( )
的最小值为( )



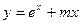 有极值,则实数m的取值范围是
有极值,则实数m的取值范围是