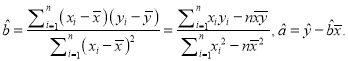题目内容
【题目】从集合
中，抽取三个不同的元素构成子集
.
（1）求对任意的
满足
的概率；
（2）若
成等差数列，设其公差为
，求随机变量
的分布列与数学期望.
【答案】（1）
.
（2）随机变量
的分布列如下：
.
【解析】（1）根据题意，由组合数计算公式、古典概型概率的计算公式进行运算即可；（2）根据题意采用列举法，将满足题意的等差数列列举出来，再由分布列、数列期望的定义进行运算即可.
试题解析：（1）由题意知基本事件数为
，
而满足条件
，即取出的元素不相邻，
则用插空法，有
种可能，
故所求事件的概率
.
（2）分析
成等差数列的情况；
的情况有7种: 
， 
， 
， 
， 
， 
， 
；
的情况有5种： 
， 
， 
， 
， 
；
的情况有3种： 
， 
， 
；
的情况有1种： 
.
故随机变量
的分布列如下：
因此， 
.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】近年来空气质量逐步恶化，雾霾天气现象增多，大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解心肺疾病是否与性别有关，在市第一人民医院随机对入院50人进行了问卷调查，得到了如表的列联表：
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为
.
（1）请将上面的列联表补充完整；
（2）是否有99%的把握认为患心肺疾病与性别有关？说明你的理由.
参考格式：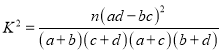 
，其中
.
下面的临界值仅供参考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差x (℃) | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．
(1)若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求出y关于x的线性回归方程
＝
x＋
；
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问(1)中所得的线性回归方程是否可靠？
附： 