题目内容
已知二次函数y=f(x)在x=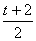 处取得最小值-
处取得最小值-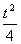 (t﹥0),f(1)=0, (1)求y=f(x)的表达式;(2)若任意实数x都满足等式f(x)g(x)+anx+bn=xn+1 (g(x)为多项式,n∈N+)试用t表示an和bn;(3)设圆Cn的方程为(x-an)2+(y-bn)2=r
(t﹥0),f(1)=0, (1)求y=f(x)的表达式;(2)若任意实数x都满足等式f(x)g(x)+anx+bn=xn+1 (g(x)为多项式,n∈N+)试用t表示an和bn;(3)设圆Cn的方程为(x-an)2+(y-bn)2=r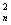 ,圆Cn与Cn+1
外切(n=1,2,3…),{rn}是各项都为正数的等比数列,记Sn为前n个圆的面积之和,求rn,sn。
,圆Cn与Cn+1
外切(n=1,2,3…),{rn}是各项都为正数的等比数列,记Sn为前n个圆的面积之和,求rn,sn。
【答案】
解:(1)设f(x)=a(x-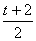 )2-
)2-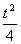 ,因为f(1)=0,所以a(1-
,因为f(1)=0,所以a(1-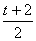 )2-
)2-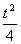 =0,得a=1,
=0,得a=1,
∴f(x)=x2-(t+2)x+t+1
(2) f(x)=(x-1)[x-(t+1)],代入已知等式得
(x-1)[x-(t+1)]g(x)+ anx+bn=xn+1
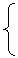 将x=1,x=t+1代入上式得
an+bn=1
将x=1,x=t+1代入上式得
an+bn=1
(t+1)an+bn=(t+1)n+1
由t≠0可得 an=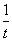 [(t+1)n+1-1],bn=
[(t+1)n+1-1],bn=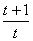 [1-(t+1)n]
[1-(t+1)n]
(3)因为an+bn=1,所以圆Cn的圆心On在直线x+y=1上,
∴︱OnOn+1︱=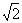 ︱an+1-an︱=
︱an+1-an︱=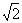 (t+1)n
(t+1)n
又∵Cn与Cn+1外切,∴rn+rn+1=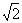 (t+1)n
(t+1)n
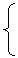 设{rn}的公比为q,则 rn+q rn=
设{rn}的公比为q,则 rn+q rn=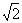 (t+1)n①
(t+1)n①
rn+1+q
rn+1=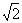 (t+1)n+1②
(t+1)n+1②
②÷①
得q=t+1,由①知r1=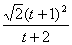

∴rn=
r1qn-1=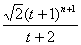
∴Sn=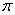 (r12+r22+…rn2)=
(r12+r22+…rn2)=
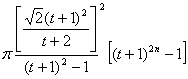
=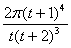

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知二次函数y=f(x)的图象如图所示:
已知二次函数y=f(x)的图象如图所示: