题目内容
比较下列两数大小
(1)0.6log23,0.6log25;
(2)lo
a,a2(a>0,且a≠1).
(1)0.6log23,0.6log25;
(2)lo
| g | a |
分析:(1)利用指数函数和对数函数的单调性即可比较出其大小;
(2)利用对数函数和幂函数的单调性即可比较出大小.
(2)利用对数函数和幂函数的单调性即可比较出大小.
解答:解:(1)∵y=log2x在(0,+∞)上为增函数,
又∵3<5,∴log23<log25.
又∵y=0.6x在R上为减函数,
∴0.6log23>0.6log25.
(2)∵logaa=1,a>0且a≠1
①当a>1时,a2>1,∴logaa<a2;
②当0<a<1时,a2<1,∴logaa>a2.
又∵3<5,∴log23<log25.
又∵y=0.6x在R上为减函数,
∴0.6log23>0.6log25.
(2)∵logaa=1,a>0且a≠1
①当a>1时,a2>1,∴logaa<a2;
②当0<a<1时,a2<1,∴logaa>a2.
点评:熟练掌握指数函数和对数函数即幂函数的单调性是解题的关键.

练习册系列答案
相关题目
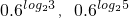 ;
;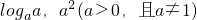 .
.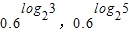 ;
;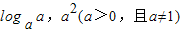 .
.