题目内容
求实数![]() 的取值范围,使关于
的取值范围,使关于![]() 的方程
的方程![]()
⑴有两个实根,且一个比2大,一个比2小;
⑵有两个实数根,且都比1大;
⑶有两实数根![]() ,
,![]() ,且满足
,且满足![]() ;
;
⑷至少有一个正根.
(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]()
解析:
设![]() ,它的图象是一条开口向上的抛物线.
,它的图象是一条开口向上的抛物线.
⑴如果函数在![]() 时的值小于零,那么抛物线就一定和
时的值小于零,那么抛物线就一定和![]() 轴有两个不同的交点,而且交点的横坐标一个比2大,一个比2小,于是由
轴有两个不同的交点,而且交点的横坐标一个比2大,一个比2小,于是由![]() ,即
,即![]() ,使得
,使得![]() .
.
⑵两个根都比1大的条件是
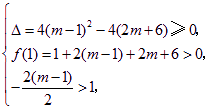 即
即
解得![]() .
.
⑶两实数根![]() ,
,![]() 满足
满足![]() 的条件是
的条件是
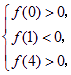 即
即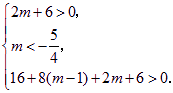
解得![]() .
.
⑷方程至少有一个正根有三种可能:
(Ⅰ)有两个正根,此时应有
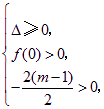 即
即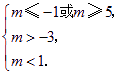
![]() .
.
(Ⅱ)有一个正根,一个负根,此时应有![]() ,解得
,解得![]() .
.
(Ⅲ)有一个正根,另一根为零,此时利用韦达定理可知
![]()
![]() ,
,
综合上述三种情况,得![]() .
.

练习册系列答案
相关题目
 :“
:“ ”,命题
”,命题 :“
:“ ”
”  的取值范围,使命题
的取值范围,使命题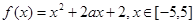
 的最小值;
的最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调函数.
上是单调函数.