题目内容
已知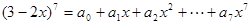 ,求(请写出最后结果):
,求(请写出最后结果):
(1)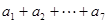 ;
;
(2)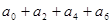 ;
;
(3)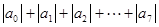 。
。
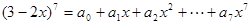 ,求(请写出最后结果):
,求(请写出最后结果):(1)
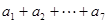 ;
;(2)
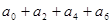 ;
;(3)
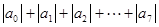 。
。(1)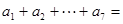
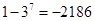 ;(2)
;(2)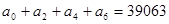 ;
;
(3)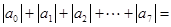
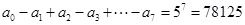 。
。
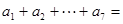
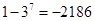 ;(2)
;(2)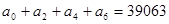 ;
;(3)
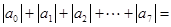
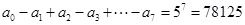 。
。本试题主要是考查了二项式定理的运用。利用赋值的思想来求解系数和的问题。
(1)先令x=0得到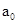 的值,然后令x=1得各个系数的和,从而得到结论。
的值,然后令x=1得各个系数的和,从而得到结论。
(2)再令x=-1,得到各项系数和,然后利用上一问的系数联立方程组得到结论。
(3)对于已知的绝对值的系数和的求解,要明白展开式中偶数项的系数都小于零,因此所求解的为奇数项系数与偶数项系数和的差,同上可得
(1)先令x=0得到
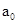 的值,然后令x=1得各个系数的和,从而得到结论。
的值,然后令x=1得各个系数的和,从而得到结论。(2)再令x=-1,得到各项系数和,然后利用上一问的系数联立方程组得到结论。
(3)对于已知的绝对值的系数和的求解,要明白展开式中偶数项的系数都小于零,因此所求解的为奇数项系数与偶数项系数和的差,同上可得

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 其中
其中 是常数,计算
是常数,计算 =______________.
=______________.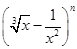 的展开式的二项式系数和为128,
的展开式的二项式系数和为128, 的值.
的值.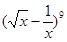 展开式中的常数项是( )
展开式中的常数项是( )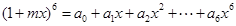 ,且
,且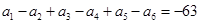 ,则实数m的值为
,则实数m的值为  的展开式中,
的展开式中,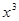 的系数是
的系数是 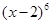 的展开式中,
的展开式中,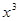 的系数是_______.
的系数是_______. = 。
= 。