题目内容
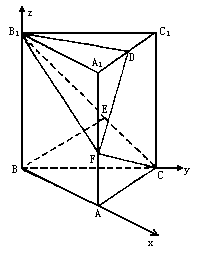
如图所示,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,E是B1C的中点.
(1)求cos( ,
, ).
).
(2)在线段AA1上是否存在点F,使CF⊥平面B1DF?若存在,求出| |;若不存在,请说明理由.
|;若不存在,请说明理由.

答案:
解析:
解析:
|
解:(1)以B为坐标原点,建立如图所示的空间直角坐标系B-xyz.
因为AC=2a,∠ABC= 所以B(0,0,0),A( 所以B1(0,0,3a),A1( 所以D( 所以 故| 又 所以cos( (2)假设存在点F,使CF⊥面B1DF,不妨设AF=b,则F( 所以 因为 所以 由 所以,当| |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
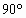 ,所以AB=BC=
,所以AB=BC=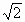 a.
a.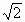 a,0,0),C(0,
a,0,0),C(0,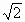 a,0),
a,0),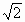 a,0,3a),C1(0,
a,0,3a),C1(0,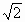 a,3a),
a,3a),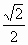 a,
a,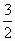 a).
a).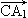 =(
=(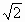 a,-
a,-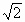 a,3a),
a,3a),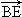 =(0,
=(0,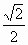 a,
a,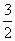 a),
a),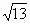 a,|
a,|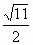 a.
a. a2=
a2=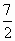 a2,
a2,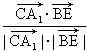 =
=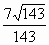 .
.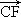 =(
=( =(
=( a,0,b-3a),
a,0,b-3a), =(
=(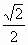 a,
a,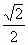 a,0).
a,0).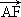 |=a或|
|=a或|
 +
+ =1(a>b>0),A,P,F分别为左顶点,上顶点,右焦点,E为x轴正方向上一点,且|
=1(a>b>0),A,P,F分别为左顶点,上顶点,右焦点,E为x轴正方向上一点,且| |,|
|,| |,|
|,| |成等比数列.又点N满足
|成等比数列.又点N满足 =
= (
( +
+ ),PF的延长线与椭圆的交点为Q,过Q与x轴平行的直线与PN的延长线交于M.
),PF的延长线与椭圆的交点为Q,过Q与x轴平行的直线与PN的延长线交于M. ·
· =
=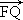 ,且|
,且| ,求椭圆方程.
,求椭圆方程.
 ,现在发现电路不通了,那么至少有两个焊接点脱落的概率是多少?
,现在发现电路不通了,那么至少有两个焊接点脱落的概率是多少?
