题目内容
.(本小题满分12分)
已知直四棱柱ABCD—A′B′C′D′的底面是菱形, ,
,
E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.
(1)求证:平面AEF⊥平面AA′C′C;
(2)求截面AEF与底面ABCD的夹角的大小.

【答案】
(1)以O为原点,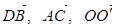 分别为x,y,z轴建立直角坐标系,由条件知:EC=BC=2,FB=1,OA=1,OB=
分别为x,y,z轴建立直角坐标系,由条件知:EC=BC=2,FB=1,OA=1,OB=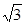 ,
,
从而坐标E(0,1,2),F(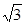 ,0,1).
,0,1).
(1)连结AE与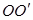 交于M,连结MF,
交于M,连结MF,
可得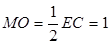 ,M(0,0,1),
,M(0,0,1),
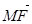 =(
=(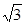 ,0,0).
,0,0).
则MF⊥平面yOz,即MF⊥平面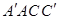 ,
,
所以平面AEF⊥平面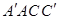 .
.
(2)取EC中点G,得平面MFG∥底面ABCD,
所以只要求面AEF与面MFG所成的二面角即可.
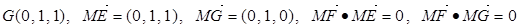
即 ,
, 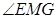 是该二面角的平面角.
是该二面角的平面角.
在Rt△MGE中,EG=1,MG=1,ME=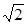 ,显然
,显然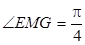 ,所求角为
,所求角为 .
.
【解析】略

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目