题目内容
已知a∈R,复数z1=
,z2=z1i(其中i表示虚数单位)
(1)z1=-i,求实数a的值;
(2)a>0且Imz2-Rez2=3,求|z2|的值.
| a-i | 1-i |
(1)z1=-i,求实数a的值;
(2)a>0且Imz2-Rez2=3,求|z2|的值.
分析:(1)由)
=-i,即可求得实数a的值;
(2)将)z2=z1•i化为:
(1-a)+
(a+1)•i,利用Imz2-Rez2=3,可求得a,从而可求得|z2|的值.
| a-i |
| 1-i |
(2)将)z2=z1•i化为:
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵
=-i,
∴a-i=-i•(1-i)=-1-i,解得 a=-1.…(2分)
(2)z2=z1•i=
•i=
(1-a)+
(a+1)•i①…(2分)
∵Imz2-Rez2=3,
∴
(1+a)-
(1-a)=3,解得a=3…(2分)
将a=3代入①得,z2=-1+2i…(2分)
则|z2|=
=
…(2分)
| a-i |
| 1-i |
∴a-i=-i•(1-i)=-1-i,解得 a=-1.…(2分)
(2)z2=z1•i=
| a-i |
| 1-i |
| 1 |
| 2 |
| 1 |
| 2 |
∵Imz2-Rez2=3,
∴
| 1 |
| 2 |
| 1 |
| 2 |
将a=3代入①得,z2=-1+2i…(2分)
则|z2|=
| 1+4 |
| 5 |
点评:本题考查复数代数形式的混合运算,关键在于掌握复数运算的性质及复数求模的方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
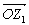 分别对应复数z1、z2,且z1=
分别对应复数z1、z2,且z1=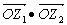 的值.
的值.