题目内容
已知函数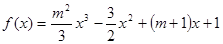
(1)若函数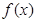 在
在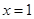 处取得极大值,求函数
处取得极大值,求函数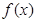 的单调区间
的单调区间
(2)若对任意实数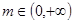 ,不等式
,不等式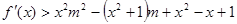 恒成立,求
恒成立,求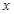 的取值范围
的取值范围
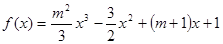
(1)若函数
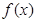 在
在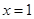 处取得极大值,求函数
处取得极大值,求函数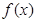 的单调区间
的单调区间(2)若对任意实数
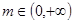 ,不等式
,不等式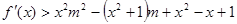 恒成立,求
恒成立,求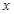 的取值范围
的取值范围(1) 函数
函数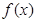 的增区间为
的增区间为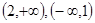 减区间为
减区间为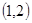 ;(2)
;(2)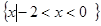 。
。
 函数
函数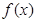 的增区间为
的增区间为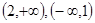 减区间为
减区间为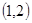 ;(2)
;(2)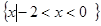 。
。试题分析:(1)
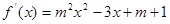 ,且在
,且在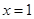 处取极大值,则
处取极大值,则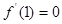
则
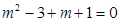 ,解得
,解得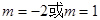
当
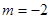 时,
时, ,在
,在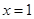 处取极小值
处取极小值当
 时,
时,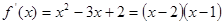 ,在
,在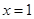 处取极大值
处取极大值所以
 函数
函数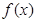 的增区间为
的增区间为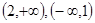 减区间为
减区间为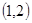
(2)因为
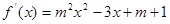 ,则
,则
即为

则有
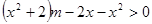 在
在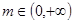 恒成立,则
恒成立,则
解得:
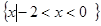
点评:中档题,本题属于导数的基本应用问题。在某区间,导数值非负,函数为增函数,导数值非正,函数为减函数。涉及不等式恒成立问题,往往通过构造函数,确定函数的最值,达到解题目的。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
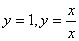

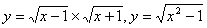
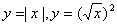
 的图象大致是
的图象大致是
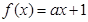 在R上递减,则函数
在R上递减,则函数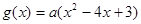 的增区间是 ( )
的增区间是 ( )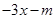
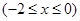 有两个不同的交点,求实数m的取值范围.
有两个不同的交点,求实数m的取值范围. 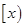 表示大于
表示大于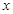 的最小整数,例如
的最小整数,例如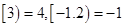 .下列命题
.下列命题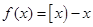 的值域是
的值域是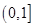 ;②若
;②若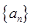 是等差数列,则
是等差数列,则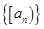 也是等差数列;
也是等差数列;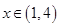 ,则方程
,则方程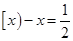 有3个根.
有3个根.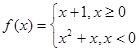 的零点的个数为 .
的零点的个数为 .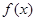 的导函数
的导函数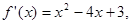 则函数
则函数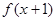 的单调递减区间是( )
的单调递减区间是( )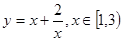 的值域为 .
的值域为 .