题目内容
函数f(x)=x3+ax2+bx在x=-1处取得极值,且f(x)的图象在P(1,f(1))处的切线平行于直线y=8x.
(I)求函数f(x)解要式和极值;
(II)对任意α,β∈R,求证|f(sinα)-f(cosβ)|≤
.
(I)求函数f(x)解要式和极值;
(II)对任意α,β∈R,求证|f(sinα)-f(cosβ)|≤
| 112 | 27 |
分析:(I)由
解出a 和 b 的值,可得函数f(x)的解析式以及其导数的解析式,
求出导数等于0的根,考查导数在根的两侧的符号,求出极值.
(II)结合 (I)求出 f(x)在[-1,1]上的最大和最小值,|f(sinα)-f(cosβ)|小于或等于
最大值减去最小值.
|
求出导数等于0的根,考查导数在根的两侧的符号,求出极值.
(II)结合 (I)求出 f(x)在[-1,1]上的最大和最小值,|f(sinα)-f(cosβ)|小于或等于
最大值减去最小值.
解答:解:(I)由
得
得
,
∴f(x)=x3+2x2+x.
则f'(x)=3x2+4x+1,由f'(x)=0得x=-1或x=-
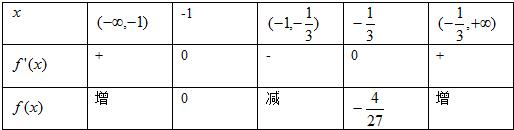
f(x)极大=f(-1)=0,f(x)极小=f(-
)=-
.
(II)∵α,β∈R,∴-1≤sinα≤1,-1≤cosβ≤1,
由(I)知f(x)在[-1,1]上的最大,最小值分别为f(1)=4,f(-
)=-
,
∴|f(sinα)-f(cosβ)|≤4-(-
)≤
.
|
|
|
∴f(x)=x3+2x2+x.
则f'(x)=3x2+4x+1,由f'(x)=0得x=-1或x=-
| 1 |
| 3 |

f(x)极大=f(-1)=0,f(x)极小=f(-
| 1 |
| 3 |
| 4 |
| 27 |
(II)∵α,β∈R,∴-1≤sinα≤1,-1≤cosβ≤1,
由(I)知f(x)在[-1,1]上的最大,最小值分别为f(1)=4,f(-
| 1 |
| 3 |
| 4 |
| 27 |
∴|f(sinα)-f(cosβ)|≤4-(-
| 4 |
| 27 |
| 112 |
| 27 |
点评:本题考查函数在某处取的价值的条件,导数与切线斜率的关系,求函数在闭区间上的最值的方法.

练习册系列答案
相关题目