题目内容
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
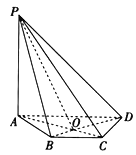
(1)证明:BD⊥PC;
(2)若AD=4,BC=2,设AC∩BD=O,且∠PDO=60°,求四棱锥P-ABCD的体积.
【答案】(1)见解析;(2)12
【解析】
(1)可证![]() 平面
平面![]() ,从而得到
,从而得到![]() .
.
(2)连结![]() ,根据
,根据![]() 可得
可得![]() ,再根据
,再根据![]() 均为等腰直角三角形得到梯形
均为等腰直角三角形得到梯形![]() 的高和
的高和![]() 的长度,从而得到
的长度,从而得到![]() 的长度后可利用体积公式计算四棱锥的体积.
的长度后可利用体积公式计算四棱锥的体积.
证明:(1)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,
,![]() 是平面
是平面![]() 内的两条相交直线,
内的两条相交直线,
所以![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,所以
,所以![]() .
.
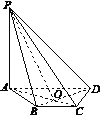
(2)连结![]() ,由(1)知,
,由(1)知,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 知,
知,![]() .在
.在![]() 中,
中,
因为![]() ,所以
,所以![]() ,得
,得![]() .
.
又因为四边形![]() 为等腰梯形,
为等腰梯形,![]() ,
,
所以![]() 均为等腰直角三角形.
均为等腰直角三角形.
从而梯形![]() 的高为
的高为![]() ,
,
于是梯形![]() 面积
面积![]() .
.
在等腰直角三角形![]() 中,
中,![]() ,
,
所以![]() ,
,![]() .
.
故四棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目