题目内容
已知f（x）=ax-lnx，a∈R．
（I）当a=2时，求曲线f（x）在点（1，f（1））处的切线方程；
（II）f（x）在x=1处有极值，求f（x）的单调递增区间；
（III）是否存在实数a，使f（x）在区间（0，e]的最小值是3？若存在，求出a的值；若不存在，说明理由．
解：（I）当a=2时，f（x）=2x-lnx，函数的定义域为（0，+∞）
求导函数可得：f′（x）=2-
∴f′（1）=1，f（1）=2
∴曲线f（x）在点（1，f（1））处的切线方程为y-2=x-1，即x-y+1=0；
（II）∵f（x）在x=1处有极值，∴f′（1）=0
∵f′（x）=a-
∴a-1=0，∴a=1
∴f′（x）=1-
令f′（x）＞0，可得x＜0或x＞1
∵x＞0，∴x＞1
∴f（x）的单调递增区间为（1，+∞）；
（III）假设存在实数a，使f（x）在区间（0，e]的最小值是3，
①当a≤0时，∵x∈（0，e]，∴f′（x）＜0，∴f（x）在区间（0，e]上单调递减
∴f（x）min=f（e）=ae-1=3，∴a=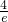
（舍去）；
②当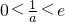
时，f（x）在区间（0，
）上单调递减，在（，e]上单调递增
∴f（x）min=f（）=1+lna=3，∴a=e3，满足条件；
③当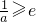
时，∵x∈（0，e]，∴f′（x）＜0，∴f（x）在区间（0，e]上单调递减
∴f（x）min=f（e）=ae-1=3，∴a=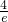（舍去），
综上所述，存在实数a=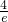，使f（x）在区间（0，e]的最小值是3．
分析：（I）当a=2时，f（x）=2x-lnx，函数的定义域为（0，+∞），求导函数，即可确定切点与切线的斜率，从而可得曲线f（x）在点（1，f（1））处的切线方程；
（II）利用f（x）在x=1处有极值，确定a的值，利用导数大于0，结合函数的定义域，即可得到f（x）的单调递增区间；
（III）分类讨论，确定函数f（x）在区间（0，e]上的单调性，从而可得函数的最小值，利用最小值是3，建立方程，即可求得结论．
点评：本题考查导数知识的运用，考查导数的几何意义，考查函数的极值与单调性，考查函数的最值，考查分类讨论的数学思想，属于中档题．
求导函数可得：f′（x）=2-
∴f′（1）=1，f（1）=2
∴曲线f（x）在点（1，f（1））处的切线方程为y-2=x-1，即x-y+1=0；
（II）∵f（x）在x=1处有极值，∴f′（1）=0
∵f′（x）=a-
∴a-1=0，∴a=1
∴f′（x）=1-
令f′（x）＞0，可得x＜0或x＞1
∵x＞0，∴x＞1
∴f（x）的单调递增区间为（1，+∞）；
（III）假设存在实数a，使f（x）在区间（0，e]的最小值是3，
①当a≤0时，∵x∈（0，e]，∴f′（x）＜0，∴f（x）在区间（0，e]上单调递减
∴f（x）min=f（e）=ae-1=3，∴a=
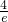（舍去）；②当
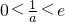时，f（x）在区间（0，）上单调递减，在（，e]上单调递增∴f（x）min=f（
）=1+lna=3，∴a=e3，满足条件；③当
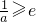时，∵x∈（0，e]，∴f′（x）＜0，∴f（x）在区间（0，e]上单调递减∴f（x）min=f（e）=ae-1=3，∴a=
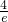（舍去），综上所述，存在实数a=
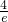，使f（x）在区间（0，e]的最小值是3．分析：（I）当a=2时，f（x）=2x-lnx，函数的定义域为（0，+∞），求导函数，即可确定切点与切线的斜率，从而可得曲线f（x）在点（1，f（1））处的切线方程；
（II）利用f（x）在x=1处有极值，确定a的值，利用导数大于0，结合函数的定义域，即可得到f（x）的单调递增区间；
（III）分类讨论，确定函数f（x）在区间（0，e]上的单调性，从而可得函数的最小值，利用最小值是3，建立方程，即可求得结论．
点评：本题考查导数知识的运用，考查导数的几何意义，考查函数的极值与单调性，考查函数的最值，考查分类讨论的数学思想，属于中档题．
练习册系列答案
相关题目