题目内容
已知f(x)=ax(a>1),g(x)=bx(b>1),当f(x1)=g(x2)=2时,有x1>x2,则a,b的大小关系是( )
分析:根据f(x)=ax(a>1),g(x)=bx(b>1),f(x1)=g(x2)=2可得ax1=2,bx2=2,然后利用对数的定义可得x1=loga2,x2=logb2再结合x1>x2利用对数函数的单调性即可比较出a,b的大小.
解答: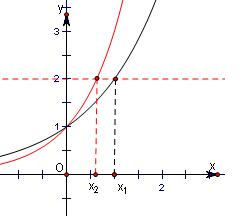 解:∵f(x)=ax(a>1),g(x)=bx(b>1),f(x1)=g(x2)=2
解:∵f(x)=ax(a>1),g(x)=bx(b>1),f(x1)=g(x2)=2
∴ax1=2,bx2=2
∴x1=loga2,x2=logb2
∵x1>x2
∴loga2>logb2
∴由换底公式可得
>
∵a>1,b>1
∴log2a>0,log2b>0
∴log2b>log2a①
∴由y=log2x的单调性可得b>a
故选C.
 解:∵f(x)=ax(a>1),g(x)=bx(b>1),f(x1)=g(x2)=2
解:∵f(x)=ax(a>1),g(x)=bx(b>1),f(x1)=g(x2)=2∴ax1=2,bx2=2
∴x1=loga2,x2=logb2
∵x1>x2
∴loga2>logb2
∴由换底公式可得
| 1 |
| log2a |
| 1 |
| log2b |
∵a>1,b>1
∴log2a>0,log2b>0
∴log2b>log2a①
∴由y=log2x的单调性可得b>a
故选C.
点评:本题主要考查了利用指数和对数函数的性质比较大小.解题的关键是要利用x1>x2得到loga2>logb2然后再利用换底公式和a,b的范围将上式等价变形为①式后可利用对数函数的单调性得出b>a.

练习册系列答案
相关题目