题目内容
椭圆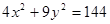 内有一点
内有一点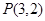 ,过点
,过点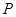 的弦恰好以
的弦恰好以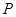 为中点,那么这条弦所在直线的斜率为 ,直线方程为 .
为中点,那么这条弦所在直线的斜率为 ,直线方程为 .
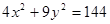 内有一点
内有一点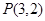 ,过点
,过点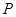 的弦恰好以
的弦恰好以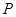 为中点,那么这条弦所在直线的斜率为 ,直线方程为 .
为中点,那么这条弦所在直线的斜率为 ,直线方程为 . ,
, (只对一个得3分)
(只对一个得3分)试题分析:本题涉及的是椭圆的弦中点问题,可用点差法.
设椭圆以
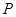 为中点的弦的两端点分别为
为中点的弦的两端点分别为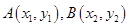 ,则
,则 ,
,
因为点
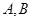 都在椭圆上,
都在椭圆上,所以,
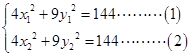
 得:
得: ,
,
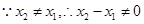
 ,
, ,解得:
,解得: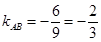 ,
,直线
 的方程为:
的方程为: ,即:
,即: .
.
练习册系列答案
相关题目
题目内容
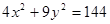 内有一点
内有一点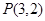 ,过点
,过点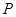 的弦恰好以
的弦恰好以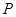 为中点,那么这条弦所在直线的斜率为 ,直线方程为 .
为中点,那么这条弦所在直线的斜率为 ,直线方程为 . ,
, (只对一个得3分)
(只对一个得3分)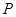 为中点的弦的两端点分别为
为中点的弦的两端点分别为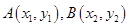 ,则
,则 ,
,
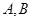 都在椭圆上,
都在椭圆上,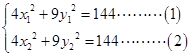
 得:
得: ,
,
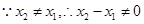
 ,
, ,解得:
,解得: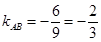 ,
, 的方程为:
的方程为: ,即:
,即: .
.