题目内容
设方程lgx+x=5的解为x0,若x0∈(k-| 1 |
| 2 |
| 1 |
| 2 |
分析:首先把方程转化成函数,利用零点的判定定理,检验函数在所给的区间上两个端点处的函数值,得到结果.
解答:解:∵lgx+x=5
∴令f(x)=lgx+x-5
∵f(1)=-4,
f(2)=lg2-3<0
f(3)=lg3-2<0
f(4)=lg4-1<0
f(5)=lg5>0
∴零点位于(4,5)上,
∵x∈(k-
,k+
)
∴k=4,
故答案为:4
∴令f(x)=lgx+x-5
∵f(1)=-4,
f(2)=lg2-3<0
f(3)=lg3-2<0
f(4)=lg4-1<0
f(5)=lg5>0
∴零点位于(4,5)上,
∵x∈(k-
| 1 |
| 2 |
| 1 |
| 2 |
∴k=4,
故答案为:4
点评:本题考查函数零点与方程的根的关系,本题解题的关键是利用函数的零点的判定定理进行验证,本题是一个基础题.

练习册系列答案
相关题目
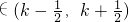 ,k∈Z,则实数k=________.
,k∈Z,则实数k=________.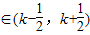 ,k∈Z,则实数k= .
,k∈Z,则实数k= .