题目内容
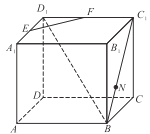
【题目】如图，在棱长为2的正方体
中，
、
分别为棱
、
的中点，
是线段
上的点，且
，若
、
分别为线段
、
上的动点，则
的最小值为__________．
【答案】
【解析】
连接B1D1交EF于G，通过证明 EF⊥平面B1D1DB可知EF⊥PG，从而PM的最小值为PG，连接BD，设其中点为H，通过△D1DB≌△D1C1B，得到PN=PH，由GH交BD1于K，则当P为K时，PM+PN取得最小值，所求最小值为GH，即可得出结论．
解：首先
的最小值就是
到
的距离.
连接
交于
，连接
，则
平面
，故
，从而的最小值，可知为的中点，
为
的四分之一.其次，连接
，在线段上取点
，使
，连接
，则
，从而
，最后，连接
交
于
，则当为时，
取得最小值，所求最小值为.
∵正方体
的棱长为2，∴
.
阅读快车系列答案
【题目】某人群中各种血型的人所占的比例见下表：
血腥 | A | B | AB | O |
该血型的人所占的比例/% | 28 | 29 | 8 | 35 |
已知同种血型的人可以互相输血，O型血可以给任一种血型的人输血，任何人的血都可以输给AB型血的人，其他不同血型的人不能互相输血.该人群中的小明是B型血，若他因病需要输血，问：
（1）任找一个人，其血可以输给小明的概率是多少？
（2）任找一个人，其血不能输给小明的概率是多少？
【题目】为了了解某市民众对某项公共政策的态度，在该市随机抽取了50名市民进行调查，作出他们的月收入（单位：百元，范围：
）的频率分布直方图，同时得到他们月收入情况以及对该项政策赞成的人数统计表：
月收入 | 赞成的人数 |
| 4 |
| 8 |
| 12 |
| 5 |
| 2 |
| 2 |
（1）求月收入在
内的频率，补全频率分布直方图，并在图中标出相应纵坐标；
（2）若从月收入在
内的被调查者中随机选取2人，求这2人对该项政策都不赞成的概率.
【题目】某公司在过去几年内使用某种型号的灯管1 000根，该公司对这些灯管的使用寿命（单位：h）进行了统计，统计结果如表所示：
分组 |
|
|
|
|
频数 | 48 | 121 | 208 | 223 |
频率 | ||||
分组 |
|
|
| |
频数 | 193 | 165 | 42 | |
频率 |
（1）将各组的频率填入表中；
（2）根据上述统计结果，估计该种型号灯管的使用寿命不足1500 h的概率.
