Question

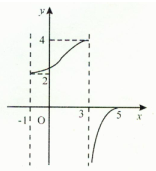（2012•武昌区模拟）函数y=f（x）的图象如图所示，给出以下说法：其中正确的是（　　）
①函数y=f（x）的定义域是[一l，5]；
②函数y=f（x）的值域是（一∞，0]∪[2，4]；
③函数y=f（x）在定义域内是增函数；
④函数y=f（x）在定义域内的导数f'（x）＞0．

A．①②

B．①③

C．②③

D．②④

Answer 1

分析：根据图象可知函数的定义域和值域，以及f（x）在[-1，3]和（3，5]上的单调性，但在定义域内不是增函数函数不单调，可得正确答案．

解答：解：由图可知f（x）的定义域为[-1，3]∪（3，5]=[-l，5]；，∴①对．
f（x）值域为（-∞，0]∪[2，4]；∴②正确．
f（x）在[-1，3]和（3，5]上是增函数，但在定义域内不是增函数，∴③错，
由于函数y=f（x）在x=3时的导数不存在，故④错．
故选A．

点评：考查学生会求函数定义域、值域的能力，会判断函数的单调性的能力，属于基础题．