题目内容
（本小题满分12
分）
设函数f(x)的定义域为R，若|f(x)|≤|x|对任意的实数x均成立，则称函数f(x)为
函数。
（1）试判断函数
=
=
中哪些是函数，并说明理由；
（2）求证：若a>1，则函数f(x)=ln(x2+a)-lna是函数。
（1）
不是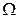
函数；（2）在R上恒有|f(x)| ≤|x|成立，则函数f(x) 是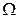函数.
解析
练习册系列答案
世纪百通期末金卷系列答案
相关题目
世纪百通期末金卷系列答案题目内容
（本小题满分12分）
设函数f(x)的定义域为R，若|f(x)|≤|x|对任意的实数x均成立，则称函数f(x)为函数。
（1）试判断函数= =中哪些是函数，并说明理由；
（2）求证：若a>1，则函数f(x)=ln(x2+a)-lna是函数。
（1）不是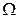函数；（2）在R上恒有|f(x)| ≤|x|成立，则函数f(x) 是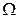函数.
解析
世纪百通期末金卷系列答案
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
