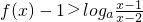题目内容
设f(x)=logax(a>0且a≠1),若f(x1)+f(x2)+…+f(xn)=1(x∈R+,i=1,2…n),则f(x13)+f(x23)+…+f(xn3)的值等于________.
3
分析:由对数的运算性质可得f(x1)+f(x2)+…+f(xn)=1?f(x1)+f(x2)+…+f(xn)=loga(x1…xn)=1,从而f(x13)+f(x23)+…+f(xn3)=loga(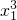 …
…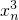 )=3loga(x1…xn)=3.
)=3loga(x1…xn)=3.
解答:∵f(x)=logax(a>0且a≠1),
∴f(x1)+f(x2)+…+f(xn)=loga(x1…xn)=1,
∴f(x13)+f(x23)+…+f(xn3))=loga(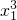 …
…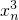 )=3loga(x1…xn)=3.
)=3loga(x1…xn)=3.
故答案为:3.
点评:本题考查对数的运算性质,熟练掌握对数的运算性质是解决问题的关键,属于基础题.
分析:由对数的运算性质可得f(x1)+f(x2)+…+f(xn)=1?f(x1)+f(x2)+…+f(xn)=loga(x1…xn)=1,从而f(x13)+f(x23)+…+f(xn3)=loga(
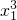 …
…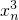 )=3loga(x1…xn)=3.
)=3loga(x1…xn)=3.解答:∵f(x)=logax(a>0且a≠1),
∴f(x1)+f(x2)+…+f(xn)=loga(x1…xn)=1,
∴f(x13)+f(x23)+…+f(xn3))=loga(
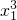 …
…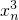 )=3loga(x1…xn)=3.
)=3loga(x1…xn)=3.故答案为:3.
点评:本题考查对数的运算性质,熟练掌握对数的运算性质是解决问题的关键,属于基础题.

练习册系列答案
相关题目