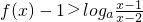题目内容
设f(x)=loga(x-2a)+loga(x-3a),其中a>0且a≠1.
(1)已知f(4a)=1,求a的值;
(2)若在区间[a+3,a+4]上f(x)≤1恒成立,求a的取值范围.
(1)已知f(4a)=1,求a的值;
(2)若在区间[a+3,a+4]上f(x)≤1恒成立,求a的取值范围.
分析:(1)将x=4a代入f(x)中,列出等式,利用对数的运算性质化简求值,即可求出a的值;
(2)利用对数的运算性质化简函数f(x)=loga[(x-
)2-
],求出函数的定义域,判断出内函数g(x)=(x-
)2-
在[a+3,a+4]上单调递增,将函数在区间[a+3,a+4]上f(x)≤1恒成立,转化为f(x)max≤1,再对底数a进行分类讨论,分别求出f(x)max,从而求得a的取值范围.
(2)利用对数的运算性质化简函数f(x)=loga[(x-
| 5a |
| 2 |
| a2 |
| 4 |
| 5a |
| 2 |
| a2 |
| 4 |
解答:解:(1)∵f(x)=loga(x-2a)+loga(x-3a),
∴f(4a)=loga2a+logaa=1,
∴loga2a=0,即2a=1,
∴a=
.
(2)f(x)=loga(x-2a)+loga(x-3a)=loga(x2-5ax+6a2)=loga[(x-
)2-
],
根据题意可知,
,解得,x>3a,
∴a+3>3a,即a<
,
∴(a+3)-
=
(a-2)>0,
∴g(x)=(x-
)2-
在区间[a+3,a+4]上单调递增.
①若0<a<1,则f(x)在区间[a+3,a+4]上单调递减,
∴f(x)在区间[a+3,a+4]上的最大值为f(a+3)=loga(2a2-9a+9),
∵不等式f(x)≤1在x∈[a+3,a+4]恒成立,等价于f(x)max≤1,即loga(2a2-9a+9)≤1,
∴2a2-9a+9≥a,解得a≥
或a≤
,
又∵0<a<1,
∴0<a<1.
②若1<a<
,则f(x)在区间[a+3,a+4]上单调递增,
∴f(x)在区间[a+3,a+4]上的最大值为f(a+4)=loga(2a2-12a+16),
∵不等式f(x)≤1在x∈[a+3,a+4]恒成立,等价于f(x)max≤1,即loga(2a2-12a+16)≤1,
∴2a2-12a+16≤a,即2a2-13a+16≤0,解得
≤a≤
,
∵1<a<
且
>
,
∴a∈∅.
综合①②,a的取值范围为(0,1).
∴f(4a)=loga2a+logaa=1,
∴loga2a=0,即2a=1,
∴a=
| 1 |
| 2 |
(2)f(x)=loga(x-2a)+loga(x-3a)=loga(x2-5ax+6a2)=loga[(x-
| 5a |
| 2 |
| a2 |
| 4 |
根据题意可知,
|
∴a+3>3a,即a<
| 3 |
| 2 |
∴(a+3)-
| 5a |
| 2 |
| 3 |
| 2 |
∴g(x)=(x-
| 5a |
| 2 |
| a2 |
| 4 |
①若0<a<1,则f(x)在区间[a+3,a+4]上单调递减,
∴f(x)在区间[a+3,a+4]上的最大值为f(a+3)=loga(2a2-9a+9),
∵不等式f(x)≤1在x∈[a+3,a+4]恒成立,等价于f(x)max≤1,即loga(2a2-9a+9)≤1,
∴2a2-9a+9≥a,解得a≥
5+
| ||
| 2 |
5-
| ||
| 2 |
又∵0<a<1,
∴0<a<1.
②若1<a<
| 3 |
| 2 |
∴f(x)在区间[a+3,a+4]上的最大值为f(a+4)=loga(2a2-12a+16),
∵不等式f(x)≤1在x∈[a+3,a+4]恒成立,等价于f(x)max≤1,即loga(2a2-12a+16)≤1,
∴2a2-12a+16≤a,即2a2-13a+16≤0,解得
13-
| ||
| 4 |
13-
| ||
| 4 |
∵1<a<
| 3 |
| 2 |
13-
| ||
| 4 |
| 3 |
| 2 |
∴a∈∅.
综合①②,a的取值范围为(0,1).
点评:本题考查了对数的运算,以及复合函数的单调性和函数的恒成立问题.对于函数恒成立问题,如果能参变量分离的一般选用参变量分离的方法转化为函数的最值进行求解,否则直接运用函数的最值求解.对于对数的底数是参数的话,一般要对其进行分类讨论进行求解,运用分类讨论的数学思想方法.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目