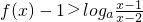题目内容
设f(x)=loga(x+1),g(x)=loga(t-x),a>0且a≠1,且F(x)=f(x)-g(x)是奇函数.
(1)若a=2,解关于x的不等式f(x)-1>loga
(2)判断F(x)的单调性,并证明.
(1)若a=2,解关于x的不等式f(x)-1>loga
| x-1 | x-2 |
(2)判断F(x)的单调性,并证明.
分析:(1)由a=2 可得不等式即 log2
>log2
,从而得
>
>0,解不等式组求得不等式的解集.
(2)由题意可得F(0)=0=loga
,求得t=1,从而F(x)=loga
,由于h(x)=
在(-1,1)上单调递增,故当a>时,F(x)单调递增;当0<a<1时,F(x)单调递减,利用单调性的定义进行证明.
| 1+x |
| 2 |
| x-1 |
| x-2 |
| x+1 |
| 2 |
| x-1 |
| x-2 |
(2)由题意可得F(0)=0=loga
| 1 |
| t |
| 1+x |
| 1-x |
| 1+x |
| 1-x |
解答:解:(1)∵a=2,∴关于x的不等式f(x)-1>loga
,
即 log2
>log2
,
∴
>
>0,
∴
,
,
,
解得 x>3,或 0<x<1,故不等式的解集为{x|x>3,或 0<x<1 }.
(2)∵F(x)=f(x)-g(x)=loga(x+1)-loga(t-x)=loga
是奇函数,
故有 F(0)=0=loga
,∴t=1,∴F(x)=loga
.
由
>0 解得-1<x<1,故F(x)的定义域为(-1,1).
由于h(x)=
在(-1,1)上单调递增,故当a>时,F(x)单调递增;当0<a<1时,F(x)单调递减.
证明:设-1<x1<x2<1,
∵h(x1)-h(x2)=
-
=
=
,
由-1<x1<x2<1,可得2x1-2x2<0,(1-x1)(1-x2)>0,
∴
<0,h(x1)<h(x2),故h(x)=
在定义域(-1,1)上单调递增,
故当a>时,F(x)单调递增;当0<a<1时,F(x)单调递减.
| x-1 |
| x-2 |
即 log2
| 1+x |
| 2 |
| x-1 |
| x-2 |
∴
| x+1 |
| 2 |
| x-1 |
| x-2 |
∴
|
|
|
解得 x>3,或 0<x<1,故不等式的解集为{x|x>3,或 0<x<1 }.
(2)∵F(x)=f(x)-g(x)=loga(x+1)-loga(t-x)=loga
| 1+x |
| t-x |
故有 F(0)=0=loga
| 1 |
| t |
| 1+x |
| 1-x |
由
| 1+x |
| 1-x |
由于h(x)=
| 1+x |
| 1-x |
证明:设-1<x1<x2<1,
∵h(x1)-h(x2)=
| 1+x1 |
| 1-x1 |
| 1+x2 |
| 1-x2 |
| (1+x1)(1-x2)-(1+x2)(1-x1) |
| (1-x1)(1-x2) |
| 2x1-2x2 |
| (1-x1)(1-x2) |
由-1<x1<x2<1,可得2x1-2x2<0,(1-x1)(1-x2)>0,
∴
| 2x1-2x2 |
| (1-x1)(1-x2) |
| 1+x |
| 1-x |
故当a>时,F(x)单调递增;当0<a<1时,F(x)单调递减.
点评:本题主要考查对数函数的单调性和特殊点,函数的单调性的判断和证明,以及函数的奇偶性的应用,属于中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目