题目内容
已知函数f(x)的定义域为D,且f(x)同时满足以下条件:
①f(x)在D上单调递增或单调递减;
②存在区间[a,b] D,使得f(x)在[a,b]上的值域是[a,b],那么我们把函数f(x)(x∈D)叫做闭函数.
D,使得f(x)在[a,b]上的值域是[a,b],那么我们把函数f(x)(x∈D)叫做闭函数.
(1)求闭函数y=-x3符合条件2的区间[a,b].
(2)判断函数y=2x-lgx是不是闭函数?若是,请说明理由,并找出区间[a,b];若不是,请说明理由.
(3)若y=k+ 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.
答案:
解析:
解析:
|
解:(1)因为y=-x3在R上单调递减,所以区间[a,b]满足 (2)取x=0.01,则y=2.02;取x=1,则y=2;取x=10,则y=19. 所以y=2x-lgx在(0,+∞)上不满足条件(1),即y=2x-lgx不是闭函数. (3)因为y=k+ 设满足条件(2)的区间为[a,b],则 即方程k+ 这等价于方程x2-(2k+1)x+k2-2=0有两个大于等于k的不相同的解. 所以 |

练习册系列答案
相关题目
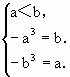 解得
解得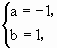 所以[a,b]=[-1,1].
所以[a,b]=[-1,1].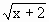 在(-2,+∞)上是单调递增的,
在(-2,+∞)上是单调递增的, 有解.
有解.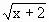 =x至少有两个不相同的解.
=x至少有两个不相同的解.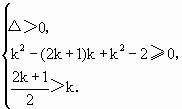 解得-
解得-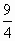 <k≤-2.所以实数k的取值范围为-
<k≤-2.所以实数k的取值范围为-