题目内容
（本题满分12分）过
与
的交点的直线被圆
所截得的弦长为
，求此直线方程。
【答案】
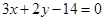或
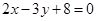
【解析】本试题主要是考查了直线与圆的位置关系的运用该。首先求出已知两条直线的交点，然后设出直线方程，利用直线方程与圆的方程联立方程值域，然后借助于韦达定理，以及相交弦的弦长公式，可知结论。
解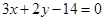： 或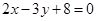
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
（本题满分12分）过与的交点的直线被圆所截得的弦长为，求此直线方程。
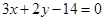或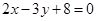
【解析】本试题主要是考查了直线与圆的位置关系的运用该。首先求出已知两条直线的交点，然后设出直线方程，利用直线方程与圆的方程联立方程值域，然后借助于韦达定理，以及相交弦的弦长公式，可知结论。
解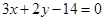： 或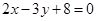
阅读快车系列答案
与椭圆C相交于两个不同点A、B，与直线2x+y-2=0交于点Q，若→AP=λ→PB，→AQ =μ→QB，求λ+μ的值
作直线
与抛物线
相交于两点
，圆
处的切线恰好与圆
相切，求直线
，
试求
的取值范围.
作倾斜角为
的直线与曲线
交于点
，求
最小值及相应的