Question

【题目】已知( ＋3x2)n的展开式中，各项系数和比它的二项式系数和大992，求：
（1）展开式中二项式系数最大的项；
（2）展开式中系数最大的项．

Answer 1

【答案】
（1）

解：令x＝1，则展开式中各项系数和为(1＋3)n＝22n.

又展开式中二项式系数和为2n，

∴22n－2n＝992，n＝5

∵n＝5，展开式共6项，二项式系数最大的项为第3、4两项，∴T3＝ C52 ( )3(3x2)2＝90x6，T4＝ C53 ( )2(3x2)3＝

（2）

解：设展开式中第r＋1项系数最大，

则Tr＋1＝C5r ( )5－r(3x2)r＝3r C5r，

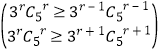∴ ,则 ，∴r＝4，

即展开式中第5项系数最大，T5＝ C54 ( )(3x2)4＝405 .

【解析】本题主要考查了二项式系数的性质，解决问题的关键是（1）利用赋值法求出各项系数和，与二项式系数和求出 值，利用二项式系数的性质求展开式中二项式系数最大的项；（2）设出展开式中系数最大的项，利用 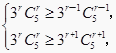进行求解即可.