题目内容
（本小题满分12分）
已知
是二次函数，
是它的导函数，且对任意的
，
恒成立．
(Ⅰ)求的解析表达式；
(Ⅱ)设
，曲线
：
在点
处的切线为
，与坐标轴围成的三角形面积为
．求的最小值．
解：(Ⅰ) 设
（
），则
， ……(2分)
．
由已知，得
，
∴
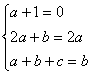，解之，得
，
，
，
∴
． ………(4分)
(Ⅱ)由（1）得，
，切线
的斜率
，
∴切线的方程为
，即
． ……………(6分)
从而
与
轴的交点为
，与
轴的交点为
，
∴
（其中
）． ……………(8分)
∴
． ………………(9分)
当
时，
，
是减函数；
当
时，
，是增函数． ……………(11分)
∴
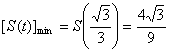． …………(12分)
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
