题目内容
已知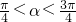 ,0<β<
,0<β< ,cos(
,cos( +α)=-
+α)=- ,sin(
,sin( +β)=
+β)= ,求sin(α+β)的值.
,求sin(α+β)的值.
解:∵ <α<
<α< ,∴
,∴ <
< +α<π.
+α<π.
又cos( +α)=-
+α)=- ,∴sin(
,∴sin( +α)=
+α)= .
.
又∵0<β< ,∴
,∴ <
< +β<π.
+β<π.
又sin( +β)=
+β)= ,∴cos(
,∴cos( +β)=-
+β)=- ,
,
∴sin(α+β)=-sin[π+(α+β)]=-sin[( +α)+(
+α)+( +β)]
+β)]
=-[sin( +α)cos(
+α)cos( +β)+cos(
+β)+cos( +α)sin(
+α)sin( +β)]
+β)]
=-[ ×(-
×(- )-
)- ×
× ]=
]= .
.
所以sin(α+β)的值为: .
.
分析:根据α、β的范围,确定 +α、
+α、 +β的范围,求出sin(
+β的范围,求出sin( +α)、cos(
+α)、cos( +β)的值,利用sin(α+β)=-sin[π+(α+β)]=-sin[(
+β)的值,利用sin(α+β)=-sin[π+(α+β)]=-sin[( +α)+(
+α)+( +β)],展开,然后求出它的值即可.
+β)],展开,然后求出它的值即可.
点评:本题是基础题,考查三角函数值的求法,注意角的范围的确定,sin(α+β)=-sin[π+(α+β)]=-sin[( +α)+(
+α)+( +β)]是集合本题的根据,角的变换技巧,三角函数的化简求值中经常应用,注意学习和总结.
+β)]是集合本题的根据,角的变换技巧,三角函数的化简求值中经常应用,注意学习和总结.
 <α<
<α< ,∴
,∴ <
< +α<π.
+α<π.又cos(
 +α)=-
+α)=- ,∴sin(
,∴sin( +α)=
+α)= .
.又∵0<β<
 ,∴
,∴ <
< +β<π.
+β<π.又sin(
 +β)=
+β)= ,∴cos(
,∴cos( +β)=-
+β)=- ,
,∴sin(α+β)=-sin[π+(α+β)]=-sin[(
 +α)+(
+α)+( +β)]
+β)]=-[sin(
 +α)cos(
+α)cos( +β)+cos(
+β)+cos( +α)sin(
+α)sin( +β)]
+β)]=-[
 ×(-
×(- )-
)- ×
× ]=
]= .
.所以sin(α+β)的值为:
 .
.分析:根据α、β的范围,确定
 +α、
+α、 +β的范围,求出sin(
+β的范围,求出sin( +α)、cos(
+α)、cos( +β)的值,利用sin(α+β)=-sin[π+(α+β)]=-sin[(
+β)的值,利用sin(α+β)=-sin[π+(α+β)]=-sin[( +α)+(
+α)+( +β)],展开,然后求出它的值即可.
+β)],展开,然后求出它的值即可.点评:本题是基础题,考查三角函数值的求法,注意角的范围的确定,sin(α+β)=-sin[π+(α+β)]=-sin[(
 +α)+(
+α)+( +β)]是集合本题的根据,角的变换技巧,三角函数的化简求值中经常应用,注意学习和总结.
+β)]是集合本题的根据,角的变换技巧,三角函数的化简求值中经常应用,注意学习和总结. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.