题目内容
（2013•湛江二模）设F1，F2是椭圆
+
=1(a＞b＞0)的左右焦点，若直线x=ma （m＞1）上存在一点P，使△F2PF1是底角为30°的等腰三角形，则m的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
分析：利用△F2PF1是底角为30°的等腰三角形，可得|PF2|=|F2F1|，根据P为直线x=ma上一点，可建立方程，由此可求椭圆的离心率的范围．
解答：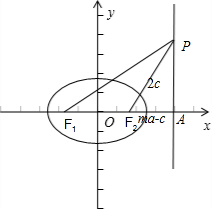
解：∵△F2PF1是底角为30°的等腰三角形
∴|PF2|=|F2F1|
∵P为直线x=ma上一点，所以∠PF2A=60°
∴cos60°=
=
，即e=
∈（0，1）
∴m∈（1，2）
故选A．
解：∵△F2PF1是底角为30°的等腰三角形∴|PF2|=|F2F1|
∵P为直线x=ma上一点，所以∠PF2A=60°
∴cos60°=
| AF2 |
| PF2 |
| ma-c |
| 2c |
| m |
| 2 |
∴m∈（1，2）
故选A．
点评：本题考查椭圆的几何性质，解题的关键是确定几何量之间的关系，属于基础题
练习册系列答案
相关题目
（2013•湛江二模）如图，已知平面上直线l1∥l2，A、B分别是l1、l2上的动点，C是l1，l2之间一定点，C到l1的距离CM=1，C到l2的距离CN=