题目内容
【题目】如图一,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() 为侧棱
为侧棱![]() 上一点,且该四棱锥的俯视图和侧视图如图二所示.
上一点,且该四棱锥的俯视图和侧视图如图二所示.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
试题分析:(1)由勾股定理可得BC⊥BD,再由线面垂直性质定理得BC⊥PD,因此由线面垂直判定定理得BC⊥平面PBD,最后根据面面垂直判定定理得结论(2)根据条件建立空间直角坐标系,设立各点坐标,通过解方程组求得各面法向量,利用向量数量积求法向量夹角,最后根据向量夹角与二面角关系求结果
试题解析:(Ⅰ)证:由俯视图可得![]()
∴BC⊥BD
又PD⊥平面ABCD,∴BC⊥PD
而PD∩BD=D,故BC⊥平面PBD
∵BC平面PBC
∴平面PBC⊥平面PBD.
(Ⅱ)解:由侧视图可得MD = 3
由俯视图及ABCD是直角梯形得:
![]()
∴![]()
以![]() 为x轴、y轴、z轴建立的空间直角坐标系D-xyz,
为x轴、y轴、z轴建立的空间直角坐标系D-xyz,
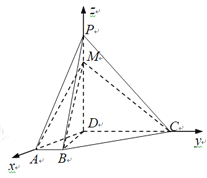
则D(0,0,0),A(![]() ,0,0),B(
,0,0),B(![]() ,1,0),C(0,4,0),M(0,0,3)
,1,0),C(0,4,0),M(0,0,3)
![]()
设平面AMB的法向量为n1 = (x1,y1,z1),则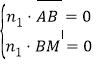 ,即
,即
令![]() ,则
,则![]() ,∴
,∴![]() 是平面AMB的一个法向量
是平面AMB的一个法向量
设平面BMC的法向量为n2 = (x2,y2,z2),则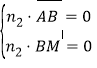 ,即
,即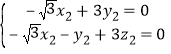
令x2 = 3,则![]() ,∴
,∴![]() 是平面BMC的一个法向量
是平面BMC的一个法向量
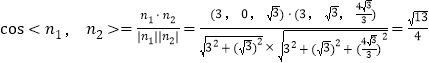
又由图可知,二面角A-BM-C为钝二面角
∴二面角A-BM-C的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
附: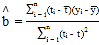 ,
,![]() . 参考数据:
. 参考数据: ![]()
