题目内容
已知函数 ,
, .
.
(1)设 是函数
是函数 的一个零点,求
的一个零点,求 的值;
的值;
(2)求函数 的单调递增区间.
的单调递增区间.
 ,
, .
.(1)设
 是函数
是函数 的一个零点,求
的一个零点,求 的值;
的值;(2)求函数
 的单调递增区间.
的单调递增区间.(1)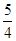 (2)
(2)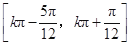 (
(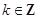 )
)
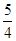 (2)
(2)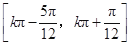 (
(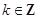 )
) 试题分析:
(1)要求
 的值,得先找到
的值,得先找到 的值;根据
的值;根据 是函数
是函数 的一个零点,所以令函数
的一个零点,所以令函数
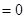 ,显然得先将函数化简,根据函数式的结构特点,利用余弦二倍角公式将其化简.而后求零点,求
,显然得先将函数化简,根据函数式的结构特点,利用余弦二倍角公式将其化简.而后求零点,求 的值.
的值.(2)首先化简函数
 式,利用辅助角公式将其化简.而后根据正弦函数的增区间
式,利用辅助角公式将其化简.而后根据正弦函数的增区间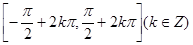 ,解得函数
,解得函数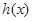 的增区间.
的增区间.试题解析:
(1)根据余弦二倍角公式有

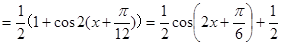
因为
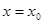 是函数
是函数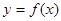 的一个零点,所以
的一个零点,所以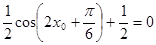 .
.即
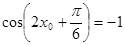 ,解得
,解得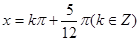 .
.所以
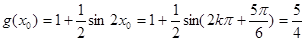 .
.(2)根据题意有
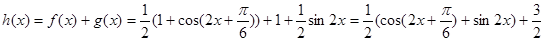
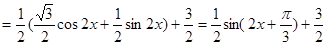
当
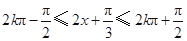 ,
, 即
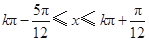 (
(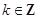 )时,
)时, 函数
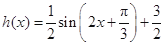 是增函数,
是增函数, 故函数
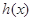 的单调递增区间是
的单调递增区间是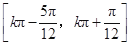 (
(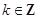 )
) 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,②图象关于直线
,②图象关于直线 对称”的一个函数是( )
对称”的一个函数是( )



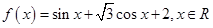
 的最小正周期;
的最小正周期; 的值.
的值. 的单调增区间
的单调增区间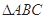 的内角
的内角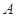 ,满足
,满足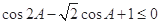 .
.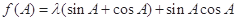 的最小值.
的最小值. 的图像向右平移
的图像向右平移 个单位可以得到函数
个单位可以得到函数 的图像,若
的图像,若 的值为( )
的值为( )

 或
或
 或
或
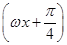 (x∈R,ω>0)的最小正周期为π,将y=f(x)的图象向左平移|φ|个单位长度,所得图象关于y轴对称,则φ的一个值是( )
(x∈R,ω>0)的最小正周期为π,将y=f(x)的图象向左平移|φ|个单位长度,所得图象关于y轴对称,则φ的一个值是( )



 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的函数图象,则下列说法正确的是( )
的函数图象,则下列说法正确的是( ) 是奇函数
是奇函数
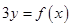 的图像关于直线
的图像关于直线 对称
对称 对称
对称
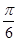 个单位,所得到的函数是偶函数;
个单位,所得到的函数是偶函数;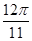 )<f(
)<f(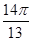 );
);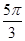 -x).
-x). 若对任意的
若对任意的 都有
都有 ,则
,则 =__________.
=__________.