题目内容
已知不等式
≥16对任意θ∈R且θ≠kπ，θ≠kπ+
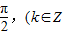）恒成立，则正实数m的最小值为： ．
【答案】分析：先由柯西不等式得：（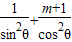
）（sin2θ+cos2θ）≥（1+
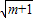）2 即
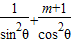≥（1+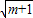
）2，再结合题中条件得出：（1+
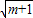）2≥16，从而得出正实数m的最小值．
解答：解：由柯西不等式得：
（
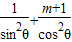）（sin2θ+cos2θ）≥（1+
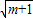）2
即
≥（1+
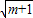）2
∵不等式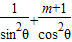
≥16对任意θ∈R且θ≠kπ，θ≠kπ+
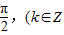）恒成立，
∴（1+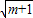
）2≥16，
∴m≥8
则正实数m的最小值为8
故答案为：8．
点评：本小题主要考查柯西不等式、恒成立问题、不等式的解法等基础知识，考查运算求解能力与转化思想．属于基础题．
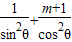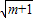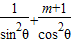）（sin2θ+cos2θ）≥（1+）2 即≥（1+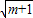）2，再结合题中条件得出：（1+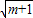）2≥16，从而得出正实数m的最小值．解答：解：由柯西不等式得：
（
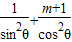）（sin2θ+cos2θ）≥（1+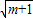）2即
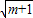≥（1+）2∵不等式
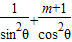≥16对任意θ∈R且θ≠kπ，θ≠kπ+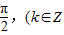）恒成立，∴（1+
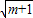）2≥16，∴m≥8
则正实数m的最小值为8
故答案为：8．
点评：本小题主要考查柯西不等式、恒成立问题、不等式的解法等基础知识，考查运算求解能力与转化思想．属于基础题．
练习册系列答案
相关题目
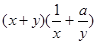≥9对任意实数
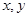恒成立，则正实数
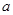的最小值为（ ）
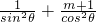≥16对任意θ∈R且θ≠kπ，θ≠kπ+
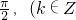）恒成立，则正实数m的最小值为：________．
+
≤2a对任意x∈[-3，1]恒成立，则实数a的取值范围为（ ）
,若对任意
及
该不等式恒成立，则实
的取值范围是 ▲ 。